Mineur complémentaire d’une matrice
Le mineur complémentaire d’un élément \( a_{ij} \) d’une matrice \( A \) est défini comme le déterminant de la sous-matrice carrée \( A_{(ij)} \), obtenue en supprimant la ligne \( i \) et la colonne \( j \) de la matrice initiale.

Comment calculer le mineur complémentaire d’un élément ?
Pour déterminer le mineur complémentaire de \( a_{ij} \) dans la matrice \( A \), on élimine la \( i \)-ème ligne ainsi que la \( j \)-ème colonne.
On obtient alors la sous-matrice complémentaire \( A_{(ij)} \).

L’étape suivante consiste à calculer le déterminant de la sous-matrice \( A_{(ij)} \).
La valeur obtenue constitue le mineur complémentaire de l’élément \( a_{ij} \).
Exemple de calcul
Considérons la matrice carrée d’ordre 3 suivante :
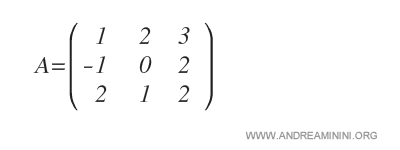
Nous cherchons à calculer le mineur complémentaire de l’élément \( a_{11} \).
Pour ce faire, on supprime la première ligne (\( i = 1 \)) et la première colonne (\( j = 1 \)).
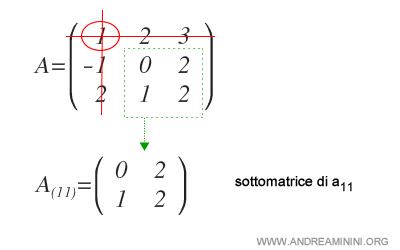
On calcule ensuite le déterminant de la sous-matrice \( A_{(11)} \).
Ce résultat correspond au mineur complémentaire de \( a_{11} \).
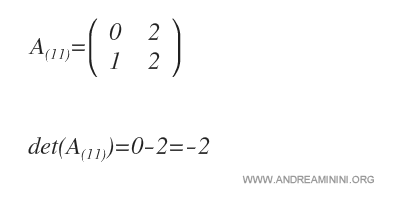
Dans ce cas précis, le mineur complémentaire est égal à 2.
Remarque : Cette méthode s’applique de la même manière à tout autre élément de la matrice \( A \), afin d’en déterminer le mineur complémentaire correspondant.