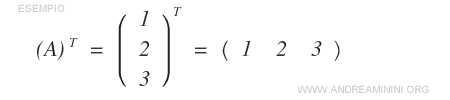Transposée d’une matrice

Qu’entend-on par transposée d’une matrice ?

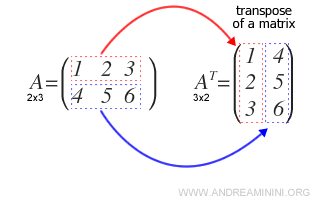
La transposée d’une matrice s’obtient en échangeant ses lignes et ses colonnes. Si \( A = (a_{ij}) \) est une matrice réelle de dimension \( m \times n \), sa transposée, notée \( A^T \), est une matrice de dimension \( n \times m \).

Exemple : Pour construire la transposée \( A^T \) d’une matrice \( A \), il suffit de réécrire chacune de ses lignes sous forme de colonne.

La notation \( A^T \) est réservée à l’opération de transposition et ne doit pas être confondue avec une notation de puissance.

Dans certains ouvrages, on peut également rencontrer d’autres écritures, telles que \( t(A) \), \( A^t \) ou encore \( ^tA \).

Propriétés de la transposition

L’opération de transposition vérifie plusieurs propriétés essentielles :

1. La transposée de la somme de deux matrices est égale à la somme de leurs transposées : \( (A + B)^T = A^T + B^T \).
   
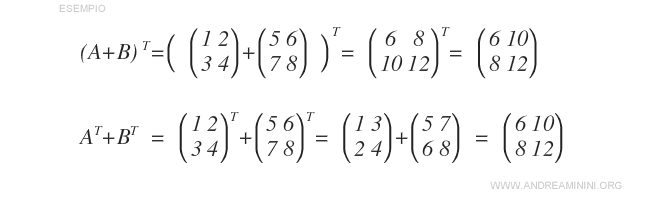
2. La transposée du produit d’un scalaire par une matrice est égale au produit de ce scalaire par la transposée de la matrice : \( (\alpha A)^T = \alpha A^T \).
   
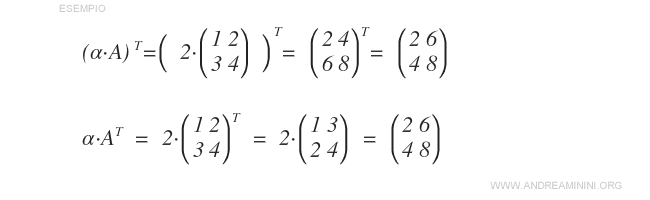
3. La transposée de la transposée d’une matrice restitue la matrice d’origine : \( (A^T)^T = A \).
   

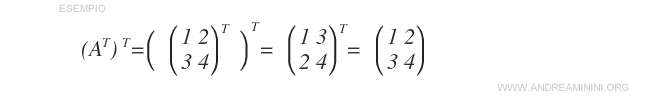
   Remarque : Cette propriété montre que la transposition est une opération involutive.

Cas particuliers

• Une matrice de dimension \( 1 \times 1 \) est égale à sa transposée.
  
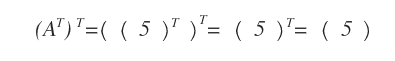
• La transposée d’une matrice ligne de dimension \( 1 \times n \) est une matrice colonne de dimension \( n \times 1 \).
  
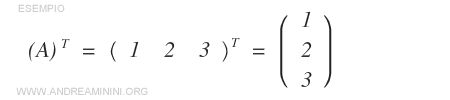
• La transposée d’une matrice colonne de dimension \( m \times 1 \) est une matrice ligne de dimension \( 1 \times m \).