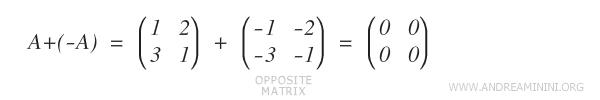Addition de matrices

Comment additionner deux matrices ?

Deux matrices A et B de mêmes dimensions (m lignes et n colonnes) s’additionnent en sommant terme à terme leurs coefficients : a_ij + b_ij. On obtient ainsi une matrice de même dimension.

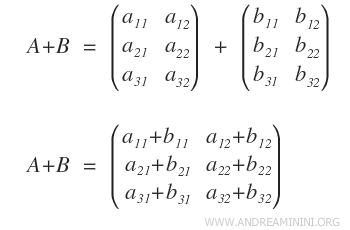
Peut-on additionner des matrices de dimensions différentes ? Non. L’addition n’est définie que lorsque les matrices possèdent le même nombre de lignes (m) et de colonnes (n).

Exemple d’addition de matrices

Considérons deux matrices A et B :

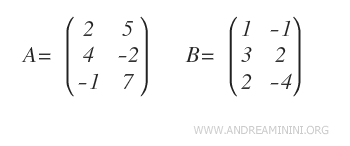
Comme elles sont toutes deux de dimension 3×2, leur somme A + B est bien définie.

La matrice A + B s’obtient en additionnant les coefficients correspondants, c’est-à-dire en calculant a_ij + b_ij pour chaque position.

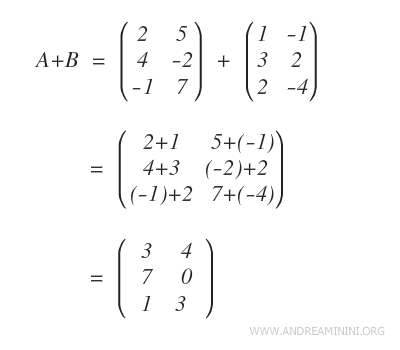
Le résultat est une nouvelle matrice qui représente la somme de A et B.

Propriétés de l’addition de matrices

L’addition matricielle satisfait aux propriétés fondamentales suivantes :

1. Associativité
   Pour trois matrices de mêmes dimensions : A + (B + C) = (A + B) + C.
2. Commutativité
   L’ordre des termes est indifférent : A + B = B + A.
   
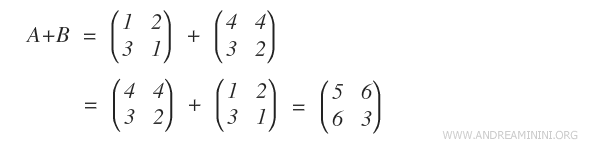
3. Élément neutre
   Il existe une matrice particulière, la matrice nulle O, telle que A + O = A pour toute matrice A.
   

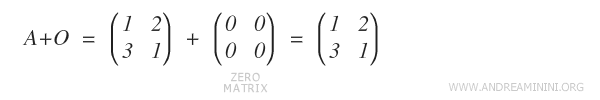
   Remarque : La matrice nulle est une matrice m×n dont tous les coefficients sont nuls.

4. Élément opposé
   À toute matrice A correspond une matrice opposée - A, vérifiant A + ( - A) = O, où O désigne la matrice nulle.