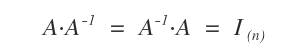Multiplication de matrices
Comment multiplie-t-on deux matrices ? En algèbre linéaire, la multiplication matricielle s’effectue selon la règle « ligne par colonne » : chaque ligne de la première matrice est combinée avec chaque colonne de la seconde.

Si Am×n est une matrice réelle et Bn×p une autre matrice réelle, leur produit est une matrice réelle Cm×p. Chaque coefficient cik de C est obtenu en sommant les produits des coefficients de la ligne i de A avec ceux de la colonne k de B.
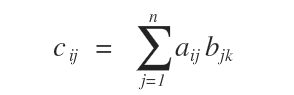
La multiplication n’est définie que si le nombre de colonnes de la première matrice est égal au nombre de lignes de la seconde.

Remarque : Autrement dit, chaque ligne de A doit avoir autant d’éléments que chaque colonne de B. L’exemple suivant l’illustre clairement.
Exemple de multiplication
Considérons deux matrices A et B.
A est de dimension 4×2 et B de dimension 2×4.
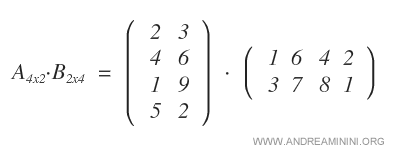
Comme le nombre de colonnes de A coïncide avec le nombre de lignes de B, le produit est défini.
Remarque : La matrice obtenue est de dimension 4×4, car elle combine les 4 lignes de A (i=4) avec les 4 colonnes de B (k=4).

On commence par multiplier chaque ligne de A par la première colonne de B, ce qui fournit la première colonne du résultat.
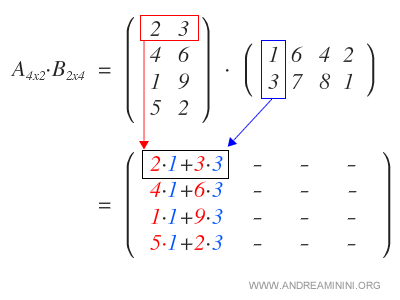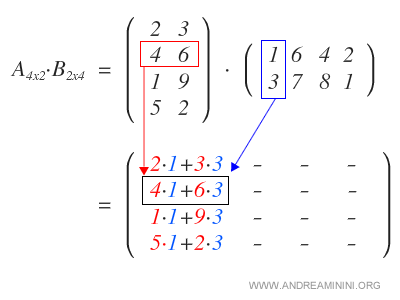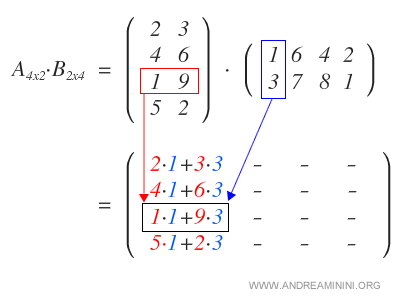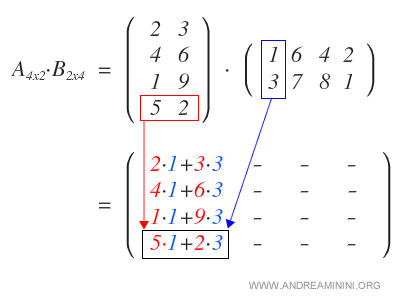
On procède de même avec la deuxième colonne de B, puis avec la troisième et la quatrième, jusqu’à compléter la matrice produit.
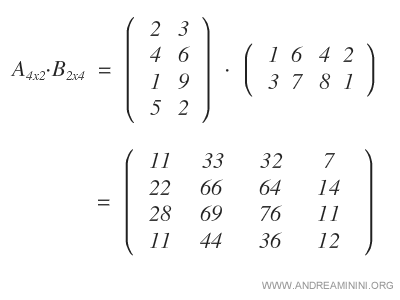
On obtient ainsi le produit matriciel A·B.
Propriétés de la multiplication de matrices
La multiplication matricielle vérifie les propriétés suivantes :
- Associativité : si A∈Mm,n, B∈Mn,p, C∈Mp,q, alors A(BC) = (AB)C.
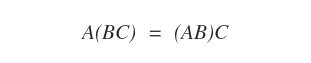
- Distributivité à droite : A(B + C) = AB + AC.
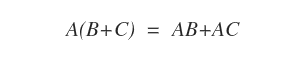
- Distributivité à gauche : (A + B)C = AC + BC.
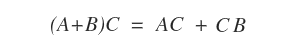
- Multiplication par un scalaire : pour α∈ℝ, α(AB) = (αA)B = A(αB).
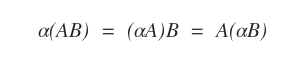
- Transposition : (AB)T = BTAT.
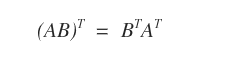
Remarque : La transposition inverse l’ordre des facteurs.
Différences avec la multiplication des réels
Non-commutativité
En général, A·B ≠ B·A.
Changer l’ordre peut donner lieu à des dimensions incompatibles, ou rendre le produit impossible.
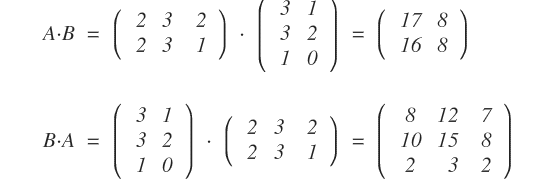
Remarque : Dans certains cas particuliers (par exemple si l’une des matrices est l’identité), on peut avoir A·B = B·A, mais cela reste exceptionnel.
Il arrive aussi que A·B soit défini mais pas B·A.

Absence de simplification
Contrairement à ℝ, on ne peut pas appliquer de règle de simplification dans l’algèbre matricielle.
Par exemple, A·0 = 0, mais deux matrices non nulles peuvent aussi avoir un produit nul.
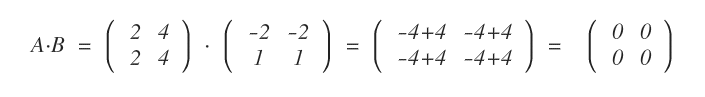
Inverse multiplicatif
Dans ℝ, tout x ≠ 0 possède un inverse 1/x tel que x·(1/x) = 1.
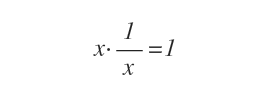
En revanche, toutes les matrices ne sont pas inversibles. Seules les matrices régulières (ou non singulières) possèdent un inverse A-1 tel que A·A-1 = I, où I est la matrice identité.
Remarque : Une matrice est inversible si et seulement si il existe A-1 vérifiant A·A-1 = I.