Matrice identité

Une matrice identité d’ordre \( n \) est une matrice carrée et diagonale dont tous les éléments de la diagonale principale valent un, tandis que toutes les autres composantes sont nulles. C’est pourquoi on l’appelle aussi matrice unité ou, plus simplement, matrice identité.

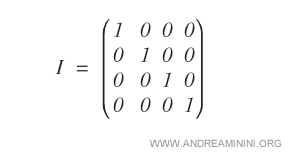
Elle constitue un cas particulier de matrice diagonale et présente des propriétés remarquables.

On la note \( I_{(n)} = (\delta_{ij}) \), où \( n \) désigne son ordre et où les éléments \( \delta_{ij} \) correspondent au delta de Kronecker.

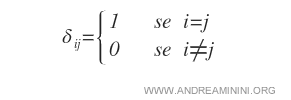
Remarque : la matrice identité est également un cas particulier de matrice scalaire, dans lequel tous les éléments de la diagonale valent exactement un.

Propriétés de la matrice identité

Voici quelques-unes de ses propriétés fondamentales :

• Elle joue le rôle d’élément neutre dans la multiplication matricielle. Pour toute matrice \( M \) ayant \( n \) colonnes, la multiplication par une matrice identité \( I \) du même ordre restitue la matrice initiale : $$ M \cdot I = M $$

  Exemple : $$ M \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

  Dans le cas de matrices non carrées, il est indispensable que le nombre de colonnes de la première coïncide avec le nombre de lignes de la seconde afin que le produit soit défini.
  • Pour toute matrice \( A \) à \( n \) colonnes : $$ A \cdot I_n = A $$

    Exemple : $$ A \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

  • Pour toute matrice \( B \) à \( n \) lignes : $$ I_n \cdot B = B $$

    Exemple : $$ I_3 \cdot A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

• Avec les matrices carrées, la matrice identité commute dans la multiplication. Si l’une des matrices \( A \) ou \( B \) est l’identité, on obtient \( AB = BA \) : l’ordre des facteurs n’influence donc pas le résultat.

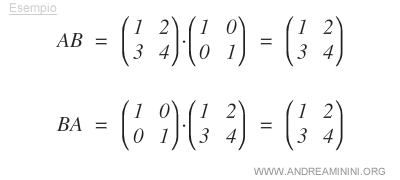
  Remarque : cette commutativité est une propriété exclusive de la matrice identité. En général, la multiplication de matrices n’est pas commutative ; voir multiplication de matrices pour plus de détails.

• Le déterminant d’une matrice identité est toujours égal à 1 : $$ \text{det}(I) = 1 $$