Puissance d’une matrice
La puissance d’une matrice se définit comme le produit successif de la matrice par elle-même, en combinant à chaque étape ses lignes avec ses colonnes.
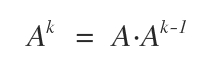
Si \( A \) est une matrice carrée d’ordre \( n \) et \( k \) un entier naturel, on appelle \( A^k \) le produit de \( A \) par elle-même répété \( k-1 \) fois.
Remarque : Élever une matrice à une puissance ne revient pas à élever séparément chacun de ses coefficients. Cette correspondance n’existe que dans certains cas particuliers, comme pour les matrices diagonales.
Exemple de calcul matriciel
Considérons la matrice carrée \( A \) d’ordre 2 ci-dessous et calculons sa troisième puissance.
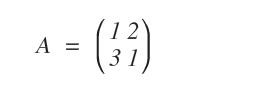
Pour obtenir \( A^3 \), on multiplie \( A \) trois fois par elle-même.
Le schéma suivant illustre cette opération étape par étape.
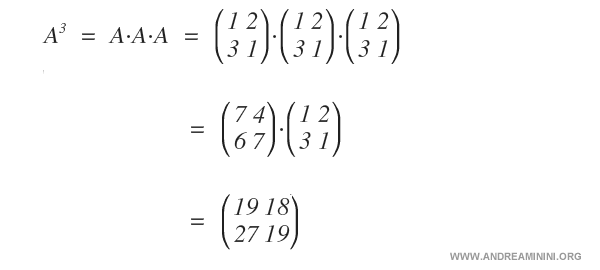
Remarque : Comme on le voit, \( A^3 \) ne consiste pas à élever chaque élément au cube, car la multiplication matricielle (ligne par colonne) obéit à des règles différentes de la multiplication scalaire.
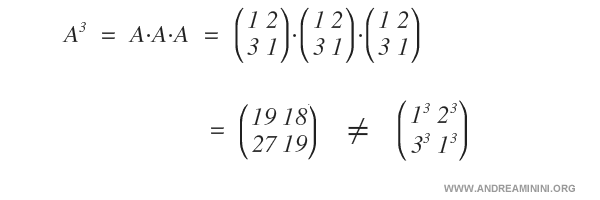
Matrices nilpotentes et idempotentes
Une matrice carrée \( A \) d’ordre \( n \) est dite nilpotente d’ordre \( k \) si \( A^k = O \), où \( O \) désigne la matrice nulle.
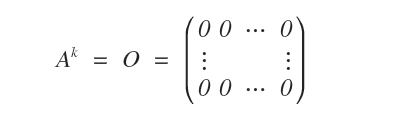
Voici un exemple de matrice nilpotente.
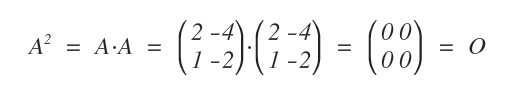
Inversement, une matrice carrée \( A \) est idempotente s’il existe un entier \( k > 0 \) tel que \( A^k = A \).

Un exemple de matrice idempotente est présenté ci-dessous.
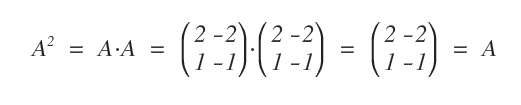
Remarque : Les notions de nilpotence et d’idempotence s’entendent uniquement dans le cadre de la multiplication matricielle, c’est-à-dire ligne par colonne.
Puissance nulle d’une matrice
Par convention, toute matrice carrée \( A \) d’ordre \( n \) élevée à la puissance zéro est définie comme la matrice identité \( I \) du même ordre.
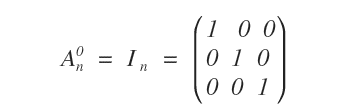
Puissances négatives d’une matrice
Si l’exposant \( k \) est négatif, la puissance \( A^k \) se définit à partir de l’inverse de \( A \), notée \( A^{-1} \), multipliée \( |k| \) fois.
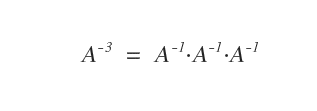
Puissances de matrices diagonales
Dans le cas particulier des matrices diagonales, calculer une puissance revient à élever chaque élément de la diagonale à l’exposant considéré. Ce comportement est propre à ce type de matrices.
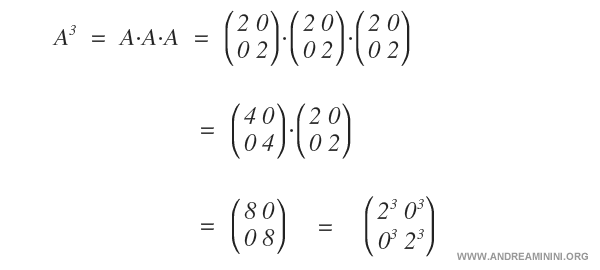
Pour les matrices non diagonales, la puissance ne s’obtient pas en élevant les coefficients individuellement.
Puissances binomiales de matrices
La formule du binôme, valable pour les nombres réels, ne s’applique pas aux matrices. La puissance matricielle obéit à ses propres règles.
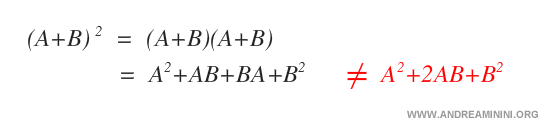
Remarque : C’est une nouvelle illustration du fait que les puissances matricielles ne suivent pas les mêmes lois que les puissances numériques et nécessitent un traitement spécifique.