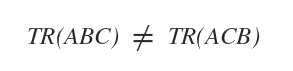Trace d’une matrice

La trace d’une matrice carrée A d’ordre n est définie comme la somme des éléments situés sur sa diagonale principale.

La formule de calcul de la trace s’écrit comme suit :

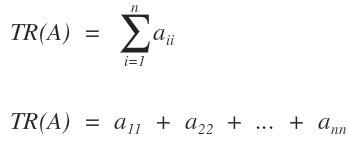
Un exemple concret

Considérons la matrice carrée suivante, de dimension 3×3 :

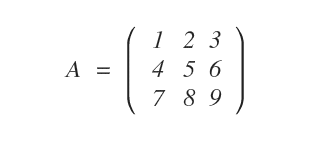
Les éléments de sa diagonale principale sont 1, 5 et 9.

Pour déterminer la trace, notée TR(A), on additionne simplement ces trois valeurs.

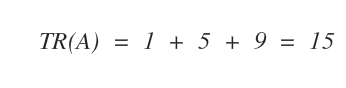
On obtient donc : la trace de la matrice A est égale à 15.

Propriétés de la trace

La trace possède plusieurs propriétés fondamentales :

1. La trace d’un produit d’un scalaire α par une matrice, TR(α·A), est égale à α multiplié par la trace de A : α·TR(A).
   
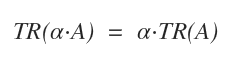
2. La trace de la somme de deux matrices est égale à la somme de leurs traces : TR(A + B) = TR(A) + TR(B).
   

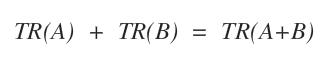
   Remarque : Ces deux premières propriétés montrent que la trace est une application linéaire.

3. Une matrice et sa transposée ont toujours la même trace : TR(A) = TR(A^T).
   
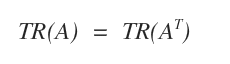
4. La trace d’un produit de matrices est invariante par permutation cyclique des facteurs : TR(ABC) = TR(BCA) = TR(CAB).
   

   Exemple de permutation non cyclique : En revanche, TR(ACB) ou TR(CBA) ne sont pas égales à TR(ABC), car il ne s’agit pas de permutations cycliques. Dans ces cas, l’ordre des facteurs ne correspond pas à un simple décalage circulaire des matrices.