Les Matrices

Introduction aux matrices

Une matrice est un tableau ordonné d’éléments a_i,j, où chaque a_i,j désigne un nombre appelé coefficient. Les indices i et j indiquent respectivement le rang de la ligne et celui de la colonne.

Lorsque les coefficients de la matrice A sont des nombres réels, on parle de matrice à coefficients réels.

Un coefficient générique (i,j) se situe sur la i-ème ligne et dans la j-ème colonne.

Les indices peuvent s’écrire avec ou sans virgule (a_m,n ou a_mn).

Remarque. L’usage de la virgule permet d’éviter les ambiguïtés lorsque les indices dépassent dix.

D’autres notations courantes pour représenter une matrice sont A_(m,n), A_mxn ou A=(a_mn).

Le couple (m, n), correspondant au nombre de lignes et de colonnes, définit la dimension de la matrice.

Ainsi, une matrice de type (m, n) possède m lignes et n colonnes.

Lorsque le nombre de lignes est égal à celui des colonnes (m = n), on obtient une matrice carrée.

À quoi sert une matrice ? Les matrices constituent un outil fondamental de l’algèbre linéaire. Elles servent notamment à représenter et à résoudre des systèmes de m équations à n inconnues.

Exemple de matrice

Considérons l’exemple suivant d’une matrice de type (2,3) :

$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$

Ses coefficients sont : $$ a_{11}=3 \\ a_{12} = 1 \\ a_{13} = 6 \\ a_{21}=0 \\ a_{22} = 4 \\ a_{23} = -1 $$

Les coefficients a₁₁, a₁₂ et a₁₃ constituent la première ligne de la matrice.

Les coefficients a₂₁, a₂₂ et a₂₃ constituent la deuxième ligne.

Remarque. En algèbre linéaire, l’ordre des coefficients est essentiel. Modifier cet ordre revient à définir une autre matrice. Par exemple, si l’on construit une matrice B en inversant les lignes de A : $$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$ $$ B : = \begin{pmatrix} 0 & 4 & -1 \\ 3 & 1 & 6 \end{pmatrix} $$ alors A et B possèdent les mêmes coefficients mais sont deux matrices distinctes. C’est un point capital à retenir.

Ensembles de matrices

L’ensemble des matrices m×n à coefficients réels (matrices réelles) se note M_m,n(ℝ) ou M(m,n,ℝ).

$$ M_{m,n}(\mathbb{R}) = M(m,n,\mathbb{R}) $$

L’ensemble des matrices carrées se note :

$$ M_{n,n}(\mathbb{R}) = M(n,n,\mathbb{R}) $$

Exemple

La matrice A a 2 lignes et 3 colonnes.

$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$

On en déduit que A appartient à l’ensemble des matrices de dimension 2×3 :

$$ A \in M(2,3,\mathbb{R}) $$

Remarque. La matrice A appartient à l’ensemble M(2,3,ℝ). Ses coefficients peuvent être entiers ou réels. Si l’on restreint aux entiers, on écrit M(2,3,ℤ), où ℤ désigne l’ensemble des entiers. On a donc M(2,3,ℤ) ⊂ M(2,3,ℝ), car à dimensions égales les entiers forment un sous-ensemble des réels.

Types de matrices

Selon leurs dimensions (nombre de lignes et de colonnes), on distingue les principaux types de matrices :

• Matrices rectangulaires. Ce sont des matrices avec m>1 et n>0, où le nombre de lignes diffère du nombre de colonnes (m≠n). Cette dissymétrie leur confère leur forme rectangulaire.
  
• Matrice carrée. Une matrice est dite carrée lorsqu’elle possède autant de lignes que de colonnes (m=n).
  
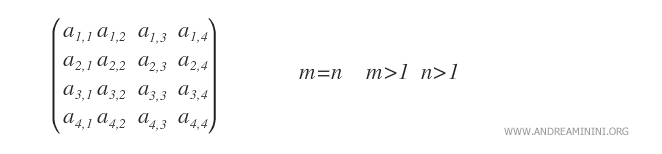
• Matrice ligne. Une matrice ligne est une matrice de type 1×n, c’est-à-dire réduite à une seule ligne.
  
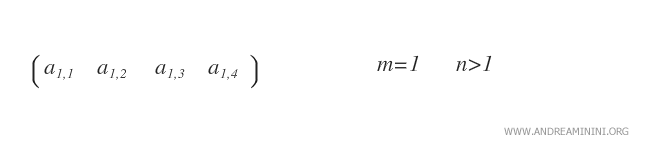
• Matrice colonne. Une matrice colonne est une matrice de type m×1, constituée d’une seule colonne.
  
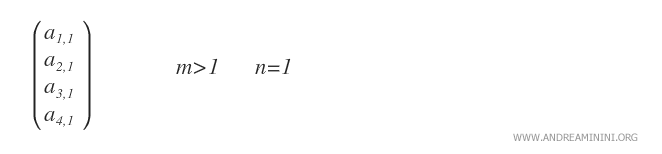
• Matrice nulle. Une matrice nulle ne contient aucun coefficient, donc ni lignes (m=0), ni colonnes (n=0).

Représentation matricielle d’un système linéaire

Considérons un système linéaire A composé de m équations à n inconnues :

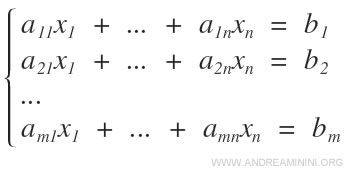
On lui associe toujours deux matrices :

1. La matrice des coefficients (ou matrice incomplète), de dimension m×n, dont les éléments sont les coefficients amn des équations.
   
2. La matrice augmentée (ou matrice complète), de dimension m×(n+1), formée des coefficients a_mn et des constantes b_m. Elle résulte de la juxtaposition de la matrice des coefficients A et du vecteur colonne B des constantes. On l’appelle aussi matrice bordée du système AX.
   

   Remarque. La matrice augmentée s’obtient en ajoutant simplement la colonne des termes constants à la matrice des coefficients.

Exemple pratique : matrices et équations en algèbre linéaire

Voici un système linéaire de deux équations à trois inconnues. Sa matrice des coefficients A est :

La matrice des coefficients A est donc :

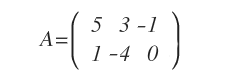
Remarque. Dans la deuxième équation (x₁−4x₂=6), la variable x₃ n’apparaît pas. On attribue alors à la position correspondante de la matrice la valeur zéro.

La matrice augmentée A|B du système est :

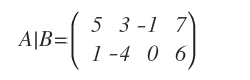
Remarque. Il suffit d’ajouter la colonne des constantes à la matrice des coefficients.

Et l’on procède de la même manière pour d’autres systèmes.