Cofacteur

Le cofacteur (ou complément algébrique) d’un élément \(a_{ij}\) d’une matrice est défini comme le déterminant de la sous-matrice \(A_{(ij)}\), obtenu en supprimant la ligne \(i\) et la colonne \(j\), puis multiplié par le facteur de signe \((-1)^{i+j}\).

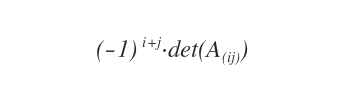
Comment calculer un cofacteur ?

Pour calculer le cofacteur d’un élément \(a_{ij}\) d’une matrice \(A\), on procède en deux étapes. On détermine d’abord son mineur associé, puis on applique le signe approprié.

Qu’est-ce qu’un mineur ? Le mineur associé à un élément \(a_{ij}\) est le déterminant de la sous-matrice obtenue en éliminant la ligne \(i\) et la colonne \(j\) de la matrice de départ.

Une fois ce mineur calculé, on le multiplie par le facteur de signe \((-1)^{i+j}\).

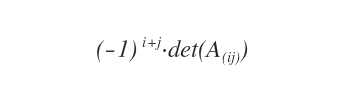
On obtient ainsi le cofacteur de \(a_{ij}\).

Le signe du cofacteur dépend uniquement de la position de l’élément dans la matrice.

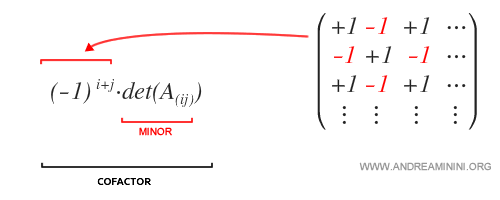
Selon la position, le cofacteur peut avoir le même signe que le mineur, ou bien l’opposé.

Exemple pratique

Considérons une matrice carrée \(A\) d’ordre 3 :

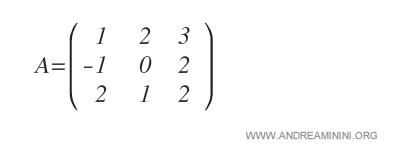
Calculons le cofacteur de l’élément \(a_{11}\).

On identifie d’abord la sous-matrice complémentaire correspondant à \(a_{11}\) :

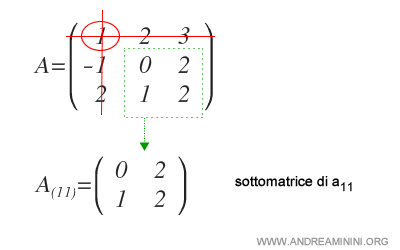
On en calcule ensuite le déterminant, qui constitue le mineur de \(a_{11}\).

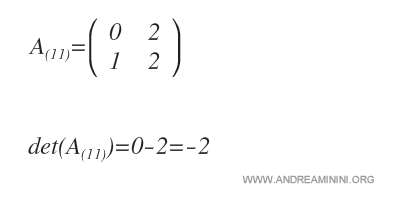
On multiplie enfin ce mineur par \((-1)^{i+j}\). Dans ce cas, comme \(i=1\) et \(j=1\), le signe est positif : \((-1)^2 = +1\).

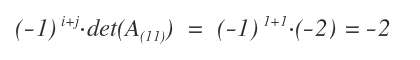
On conclut que le cofacteur de \(a_{11}\) est égal à -2.

Dans cet exemple précis, le cofacteur a la même valeur et le même signe que son mineur. Mais ce n’est pas toujours le cas, car le signe varie uniquement en fonction de la position de l’élément.

Remarque : Si l’on calcule le cofacteur de \(a_{12}\), le signe change puisque \((-1)^{1+2} = -1\). Le mineur de \(a_{12}\) vaut -6, et son cofacteur est donc égal à 6.

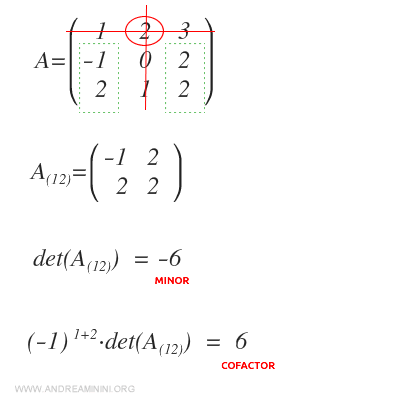
En répétant ce procédé, on peut déterminer les cofacteurs de tous les éléments de la matrice.