Matrices antisymétriques
On appelle antisymétrique une matrice \( M \) lorsque les éléments situés au-dessus de la diagonale principale sont l’opposé exact de ceux placés symétriquement au-dessous.
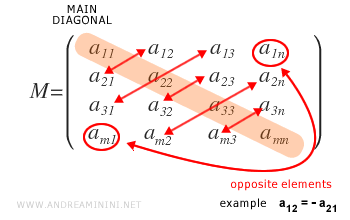
Une matrice antisymétrique se note généralement \( A^{SM} \), où AS signifie Anti Symmetric.
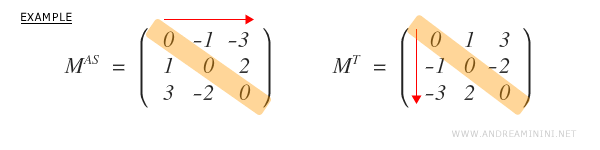
Exemple : La matrice d’ordre 3 ci-dessous illustre clairement la définition : chaque coefficient \( a_{ij} \) est l’opposé du coefficient correspondant \( a_{ji} \).
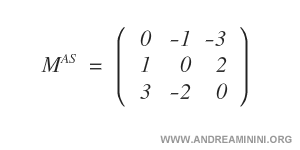
L’élément \( a_{ij} \) se déduit en échangeant la ligne et la colonne : \( a_{ij} \rightarrow a_{ji} \).
En termes généraux, pour toute matrice antisymétrique on a \( a_{ij} = -a_{ji} \), pour tout \( i, j = 1, \dots, n \).
![]()
Lien avec la transposée
Une matrice est antisymétrique si, et seulement si, sa transposée est égale à son opposée : \( M^T = -M \).
![]()
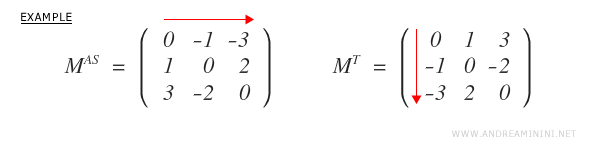
Seules les matrices carrées peuvent être antisymétriques
Une matrice non carrée ne peut pas être antisymétrique : sa transposée n’a pas les mêmes dimensions et, de plus, elle ne possède pas de diagonale principale bien définie.
Diagonal nulle
Dans toute matrice antisymétrique, les éléments de la diagonale principale sont nécessairement nuls.
Pourquoi la diagonale est-elle toujours nulle ? Parce que, dans une matrice carrée, les éléments diagonaux restent inchangés par transposition (\( a_{ii} = a_{ii} \)). L’unique solution de \( a_{ii} = -a_{ii} \) est \( a_{ii} = 0 \).
Matrice à la fois symétrique et antisymétrique ?
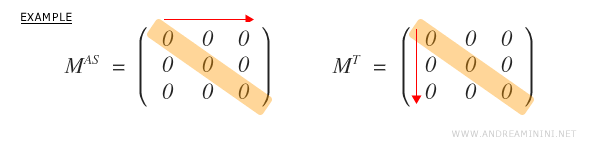
Oui, mais un seul cas est possible : la matrice nulle. C’est la seule qui satisfasse simultanément les deux conditions.
Extraction de la partie antisymétrique d’une matrice
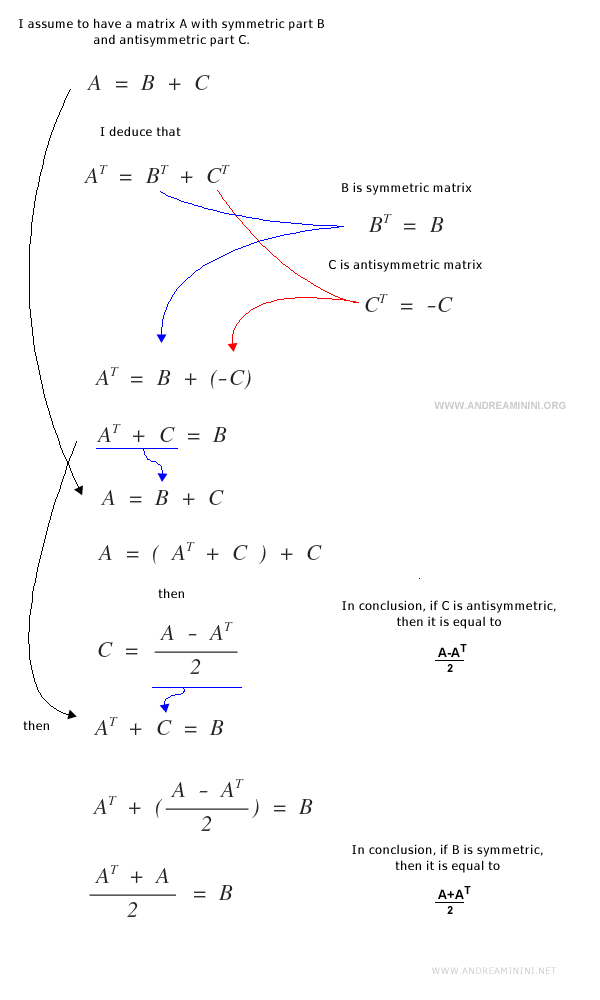
Toute matrice carrée peut être décomposée en la somme de sa partie symétrique et de sa partie antisymétrique.
La composante antisymétrique d’une matrice \( M \) se calcule à l’aide de la formule suivante :
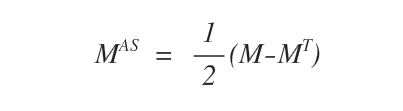
Exemple
Considérons la matrice carrée d’ordre 3 suivante, qui n’est pas antisymétrique :
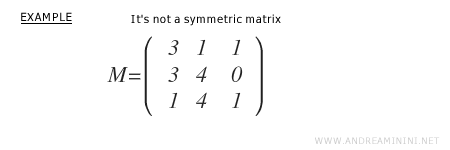
On calcule d’abord sa transposée \( M^T \).
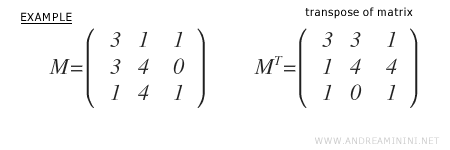
Puis on applique la formule \( \tfrac{1}{2}(M - M^T) \).
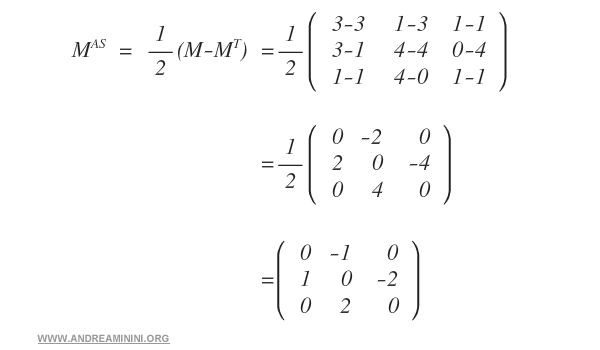
On obtient ainsi la matrice antisymétrique associée à \( M \), caractérisée par une diagonale nulle et des coefficients disposés en opposition de part et d’autre de la diagonale principale.
Décomposition en parties symétrique et antisymétrique
La somme de la partie symétrique \( M^S \) et de la partie antisymétrique \( M^{AS} \) d’une matrice carrée \( M \) reconstitue exactement \( M \).
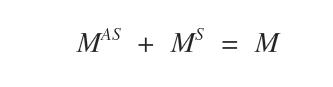
Remarque : on note \( M^{AS} \) la composante antisymétrique et \( M^S \) la composante symétrique. Si \( M \) est totalement symétrique, alors \( M^{AS} = 0 \); si elle est totalement antisymétrique, alors \( M^S = 0 \).
Voici un exemple de décomposition d’une matrice en ses deux parties :
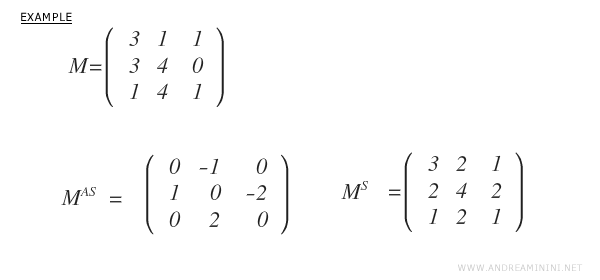
La somme de \( M^S \) et \( M^{AS} \) redonne exactement la matrice initiale \( M \).
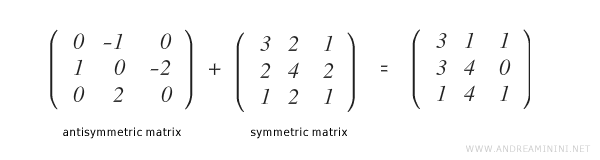
Démonstration :
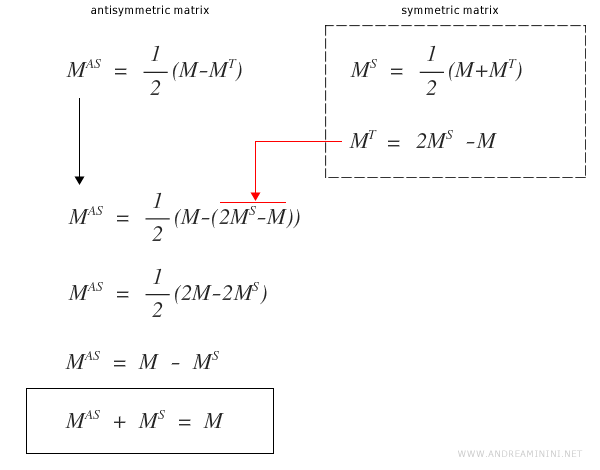
L’unicité de cette décomposition en parties symétrique et antisymétrique se justifie rigoureusement comme suit :