Matrices semblables

Dans le cadre des matrices carrées d’ordre n, on dit que deux matrices A et B sont semblables s’il existe une matrice inversible M telle que :

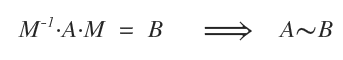
Dans ce cas, on écrit que les matrices A et B sont semblables, et l’on utilise le symbole ~ (tilde) pour indiquer cette relation.

La similitude définit une véritable relation d’équivalence sur l’ensemble des matrices carrées d’ordre n.

Propriétés des matrices semblables

1. Toute matrice est semblable à elle-même.
2. Si une matrice A est semblable à B, alors B est également semblable à A.
3. Si A est semblable à B et que B est semblable à C, alors A est semblable à C.
4. Deux matrices semblables possèdent les mêmes valeurs propres (autovaleurs), ainsi que le même déterminant, le même rang et la même trace.
5. D’un point de vue algébrique, des matrices semblables représentent le même endomorphisme par rapport à deux bases différentes B₁ et B₂ d’un même espace vectoriel V.
6. Enfin, deux matrices semblables partagent le même polynôme caractéristique.

Exemple concret de matrices semblables

Considérons les matrices A et B suivantes :

$$ A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} $$

$$ B = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Ces deux matrices sont semblables car il existe une matrice inversible M telle que :

$$ M = \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} $$

dont l’inverse est :

$$ M^{-1} = \begin{pmatrix} \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & -\frac{1}{2} \end{pmatrix} $$

et pour laquelle on vérifie :

$$ M^{-1} A M = B $$

En effet :

$$ \begin{pmatrix} \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & -\frac{1}{2} \end{pmatrix} \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$