Matrice scalaire
Une matrice scalaire est une matrice carrée dont tous les éléments de la diagonale principale sont égaux à une même constante non nulle, tandis que tous les éléments hors diagonale sont nuls.
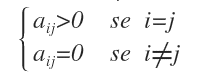
Autrement dit, il s’agit d’un cas particulier de matrice diagonale dans lequel tous les coefficients de la diagonale principale prennent exactement la même valeur.
Exemple : La matrice suivante illustre une matrice scalaire.
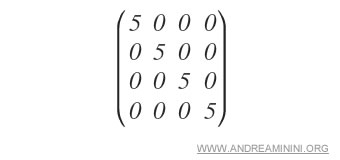
Une matrice scalaire s’obtient en multipliant la matrice identité par une constante scalaire.
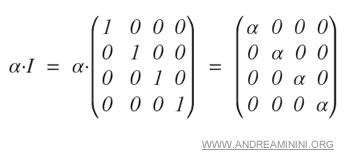
En d’autres termes, toute matrice scalaire peut toujours s’écrire comme un multiple de la matrice identité.
Si l’on note α un scalaire et I la matrice identité, une matrice scalaire n’est rien d’autre que le produit α·I.
Propriétés des matrices scalaires
Les matrices scalaires présentent une propriété fondamentale : elles commutent avec toute matrice de dimensions compatibles dans le produit matriciel.
Ainsi, pour tout nombre réel α, pour une matrice scalaire I(n) et une matrice A de dimensions compatibles, on a : α·I(n)·A = α·A·I(m), et dans les deux cas le résultat est α·A.

Exemple : Illustration pratique de l’utilisation d’une matrice scalaire.
