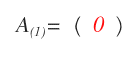Matrice carrée

Une matrice carrée est une matrice dont le nombre de lignes est égal au nombre de colonnes (m = n). On parle aussi de matrice d’ordre n, souvent notée A(n).

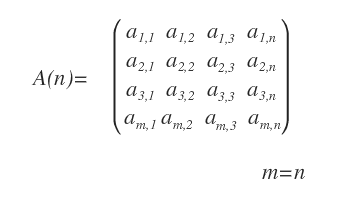
Applications des matrices carrées Les matrices carrées présentent des propriétés spécifiques qui en font des objets fondamentaux de l’algèbre linéaire.

Diagonales d’une matrice carrée

Une matrice carrée possède deux diagonales bien déterminées :

1. La diagonale principale : Dans une matrice d’ordre n, elle est formée des coefficients a_i,i (i = 1, …, n). Elle s’étend de l’angle supérieur gauche à l’angle inférieur droit.
   
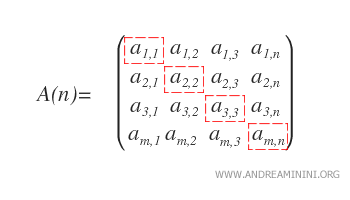
2. La diagonale secondaire : Elle est constituée des coefficients a_i,i pour i = n, …, 1, et relie l’angle supérieur droit à l’angle inférieur gauche.
   

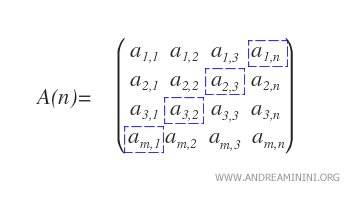
Remarque : Seules les matrices carrées possèdent des diagonales. Les matrices rectangulaires, lignes, colonnes ou nulles n’en ont pas.

Matrices triangulaires et diagonales

Selon la répartition de leurs coefficients nuls, les matrices carrées peuvent être classées en matrices triangulaires supérieures, triangulaires inférieures ou diagonales :

• Matrices triangulaires supérieures : Une matrice est triangulaire supérieure si a_ij = 0 pour tout i > j, c’est-à-dire si tous les coefficients situés en dessous de la diagonale principale sont nuls.
  
  

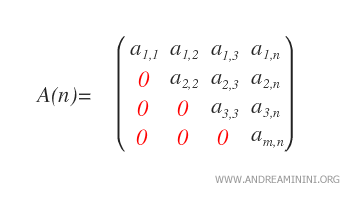
  L’ensemble des matrices triangulaires supérieures réelles d’ordre n se note U_n(ℝ).

  Matrices strictement triangulaires supérieures : Une matrice est strictement triangulaire supérieure si a_ij = 0 pour tout i ≥ j, autrement dit si tous les coefficients situés sur ou en dessous de la diagonale principale sont nuls.
  
  Cet ensemble se note U*_n(ℝ).

• Matrices triangulaires inférieures : Une matrice est triangulaire inférieure si a_ij = 0 pour tout i < j, c’est-à-dire si tous les coefficients au-dessus de la diagonale principale sont nuls.
  
  

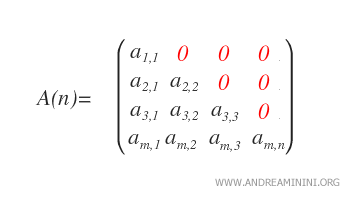
  L’ensemble des matrices triangulaires inférieures réelles d’ordre n se note L_n(ℝ).

  Matrices strictement triangulaires inférieures : Une matrice est strictement triangulaire inférieure si a_ij = 0 pour tout i ≤ j, autrement dit si tous les coefficients situés sur ou au-dessus de la diagonale principale sont nuls.
  
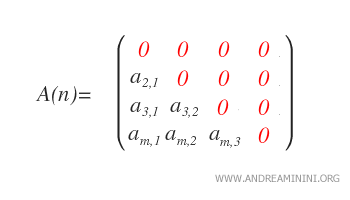
  Cet ensemble se note L*_n(ℝ).

• Matrices diagonales : Une matrice carrée est diagonale si a_ij = 0 pour tout i ≠ j, autrement dit si tous les coefficients hors de la diagonale principale sont nuls. Une matrice diagonale est donc à la fois triangulaire supérieure et triangulaire inférieure.
  
  

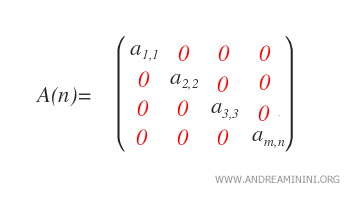
  L’ensemble des matrices diagonales réelles d’ordre n se note D_n(ℝ).

Remarque : Pour qu’une matrice soit dite triangulaire supérieure ou inférieure, il n’est pas requis que les coefficients hors de la zone de zéros soient eux-mêmes non nuls.

Cas particuliers en algèbre linéaire

Un cas notable est celui de la matrice nulle, qui satisfait simultanément aux conditions d’être triangulaire supérieure, triangulaire inférieure, strictement supérieure, strictement inférieure et diagonale.

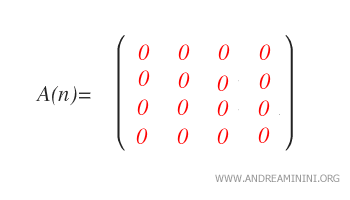
Un autre exemple est la matrice carrée d’ordre 1, constituée du seul coefficient a_1,1.

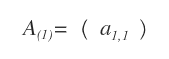
Par définition, une matrice d’ordre 1 est toujours triangulaire supérieure, triangulaire inférieure et diagonale.

Remarque : Si a_1,1 = 0, la matrice d’ordre 1 est également strictement triangulaire supérieure et strictement triangulaire inférieure.