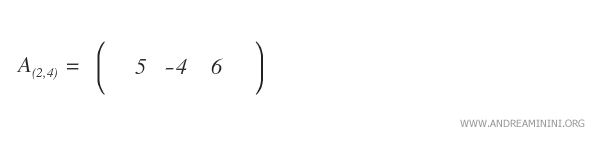Sous-matrice complémentaire

La sous-matrice complémentaire d’un élément \( a_{ij} \) est la matrice obtenue en retirant de la matrice initiale la ligne \( i \) et la colonne \( j \).

Cette sous-matrice se note généralement \( A_{(ij)} \).

Remarque : La sous-matrice complémentaire est un cas particulier de sous-matrice, défini par la suppression d’une seule ligne et d’une seule colonne.

Exemple pratique

Considérons une matrice \( A_{2\times 4} \), c’est-à-dire une matrice composée de deux lignes (\( m = 2 \)) et de quatre colonnes (\( n = 4 \)).

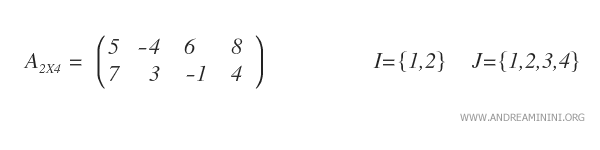
Nous voulons déterminer la sous-matrice complémentaire de l’élément \( a_{2,4} \), situé à l’intersection de la deuxième ligne et de la quatrième colonne (de valeur 4).

Pour cela, on supprime de la matrice initiale la deuxième ligne ainsi que la quatrième colonne.

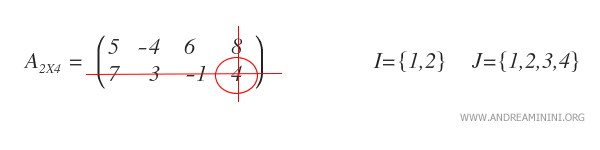
On obtient alors la sous-matrice complémentaire correspondante, notée \( A_{(2,4)} \).