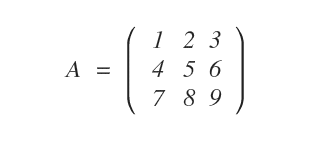Mineur d’une matrice
Le mineur d’une matrice \( A \) d’ordre \( n \) est le déterminant d’une sous-matrice carrée d’ordre \( p \) (avec \( p \leq n \)), obtenue en supprimant \( m - p \) lignes et \( n - p \) colonnes de la matrice initiale.

Il est important de souligner qu’un mineur correspond toujours au déterminant d’une sous-matrice précise (souvent appelée matrice cofacteur) : c’est donc une valeur scalaire, et non une matrice en elle-même.
Cependant, dans certains contextes, le terme « mineur » peut aussi désigner directement la sous-matrice associée.
Quel est l’ordre d’un mineur ? L’ordre d’un mineur correspond au nombre de lignes (ou de colonnes) de la sous-matrice dont on calcule le déterminant. Par exemple, une sous-matrice de trois lignes et trois colonnes engendre un mineur d’ordre trois.
Calcul d’un mineur
Pour déterminer un mineur, on sélectionne \( p \) lignes et \( p \) colonnes de la matrice \( A \), de façon à former une sous-matrice carrée.
- On identifie les lignes et colonnes à éliminer de la matrice initiale.
- La sous-matrice ainsi obtenue est appelée matrice cofacteur \( A_{ik} \).
- Le déterminant de cette sous-matrice constitue le mineur correspondant.
Remarque : Les indices \( i \) et \( j \) précisent les lignes et les colonnes exclues de \( A \) pour construire la sous-matrice carrée.
Les mineurs d’ordre un se réduisent simplement à un élément unique de la matrice d’origine.
Exemple pratique
Considérons la matrice \( 3 \times 3 \) suivante. Nous allons calculer quelques-uns de ses mineurs à titre d’illustration.
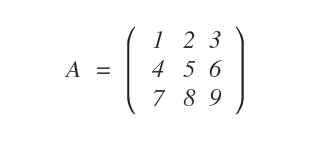
Remarque : Même si la matrice d’origine n’est pas toujours carrée, chaque mineur se calcule toujours à partir d’une sous-matrice carrée (ou d’un seul élément dans le cas d’un mineur d’ordre 1).
Cette matrice comporte trois lignes (\( m = 3 \)) et trois colonnes (\( n = 3 \)), ce qui permet de former des mineurs jusqu’à l’ordre trois.
Mineurs d’ordre deux
Pour calculer un mineur d’ordre deux (\( p = 2 \)), il faut supprimer une ligne (\( m - p = 1 \)) et une colonne (\( n - p = 1 \)).
On calcule ensuite le déterminant de la sous-matrice obtenue.

Explication : Pour obtenir le mineur \( A_{31} \), on supprime la troisième ligne (7, 8, 9) ainsi que la première colonne (1, 4, 7). Les éléments restants - situés aux lignes 1 et 2 et aux colonnes 2 et 3 - forment la sous-matrice carrée correspondante. En suivant ce même procédé, on peut déterminer les autres mineurs d’ordre deux.
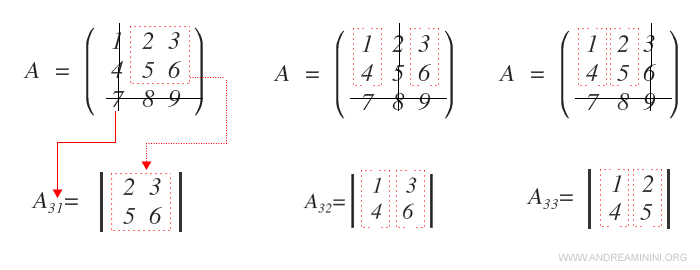
Mineurs d’ordre un
La matrice admet également neuf mineurs d’ordre un.
Pour obtenir un mineur d’ordre 1 (\( p = 1 \)), on supprime deux lignes et deux colonnes.
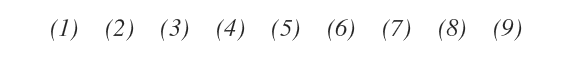
Dans ce cas, le mineur correspond simplement à la valeur de l’unique élément restant dans la sous-matrice.
Remarque : Le mineur d’ordre trois correspond au déterminant de la matrice tout entière. Pour le calculer (\( p = 3 \)), aucune ligne ni colonne n’est supprimée.