Matrices équivalentes
On dit que deux matrices sont équivalentes lorsqu’elles possèdent le même ensemble de solutions S pour leurs systèmes d’équations linéaires respectifs.
Exemple

L’équivalence entre deux matrices, M et M′, se note au moyen du symbole tilde (~).
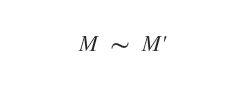
Exemple
Les matrices servent souvent à représenter des systèmes d’équations linéaires.

Réordonner les équations d’un système linéaire ne modifie pas son ensemble de solutions.
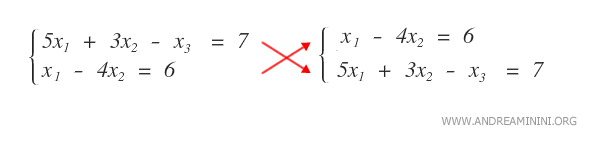
De façon analogue, permuter deux lignes d’une matrice conduit à une autre matrice équivalente.
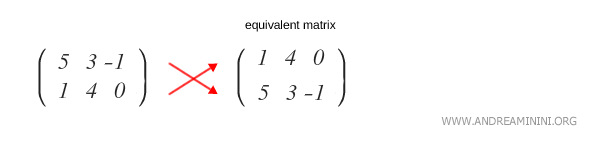
Remarque : L’exemple ci-dessus est volontairement simple afin d’illustrer l’idée. En pratique, deux matrices équivalentes peuvent présenter des coefficients très différents. Divers procédés permettent de transformer une matrice, parmi lesquels figurent l’élimination de Gauss et la variante de Gauss-Jordan.
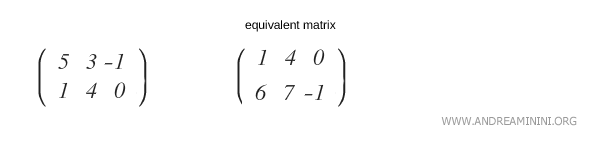
Comment obtenir une matrice équivalente
La méthode d’élimination de Gauss permet de transformer toute matrice M en une matrice équivalente M′, grâce à une suite d’opérations élémentaires appelées opérations de Gauss.
- Permuter deux lignes de la matrice
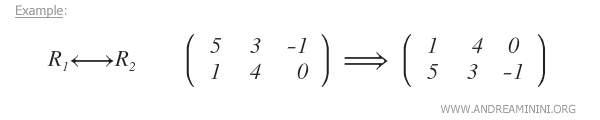
- Multiplier une ligne par un nombre réel non nul α
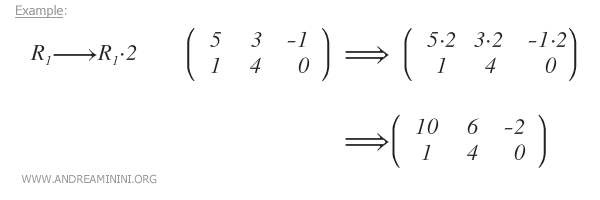
- Ajouter à une ligne un multiple d’une autre ligne
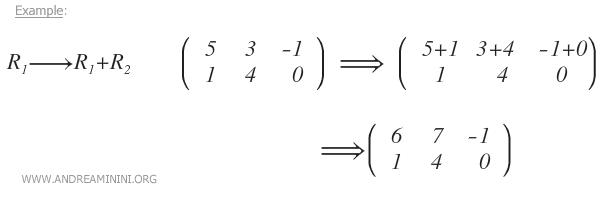
De même que la somme de deux polynômes conserve leurs zéros communs, l’addition d’une ligne avec un multiple d’une autre ne modifie pas l’ensemble des solutions du système.
Remarque : Les deux dernières opérations peuvent être combinées. On peut, par exemple, ajouter à une ligne une autre ligne préalablement multipliée par un nombre réel.