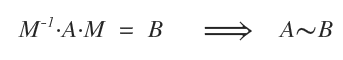Matrices (Foire aux questions)

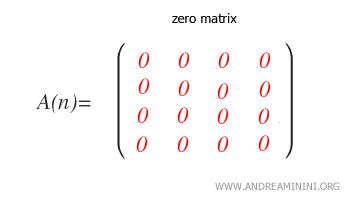
1. Qu’est-ce qu’une matrice nulle ?
   Une matrice nulle est une matrice dont tous les éléments sont égaux à zéro.
   
2. Qu’est-ce qu’une matrice carrée ?
   C’est une matrice qui possède le même nombre de lignes et de colonnes (m = n).
   
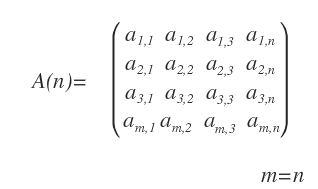
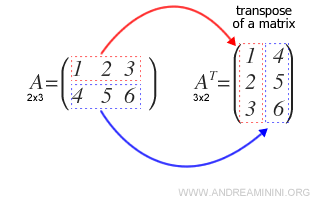
3. Qu’est-ce que la matrice transposée ?
   La transposée d’une matrice \( A^T \) s’obtient en échangeant ses lignes et ses colonnes.
   
4. Qu’est-ce que la matrice opposée ?
   Il s’agit de la matrice \(-A\), dont les éléments ont la même valeur absolue que ceux de \( A \), mais avec le signe opposé.
   
5. Que sont des matrices équivalentes ?
   Deux matrices sont dites équivalentes si elles correspondent à des systèmes linéaires ayant le même ensemble de solutions.
   
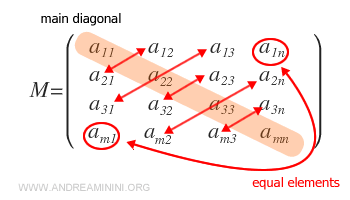
6. Qu’est-ce qu’une matrice symétrique ?
   C’est une matrice carrée dont les éléments sont symétriques par rapport à la diagonale principale, autrement dit \( a_{ij} = a_{ji} \).
   
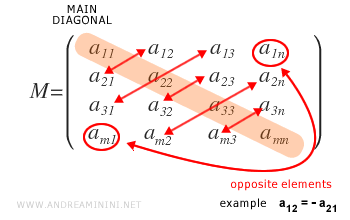
7. Qu’est-ce qu’une matrice antisymétrique ?
   C’est une matrice carrée telle que \( a_{ij} = -a_{ji} \) pour tous les éléments symétriques par rapport à la diagonale principale.
   
8. Qu’est-ce qu’une matrice diagonale ?
   C’est une matrice carrée dont tous les éléments hors de la diagonale principale sont nuls. Seuls les éléments de la diagonale peuvent être non nuls.
   
9. Qu’est-ce que la matrice identité ?
   C’est une matrice diagonale dont tous les éléments de la diagonale principale valent 1. Elle constitue un cas particulier de matrice scalaire.
   
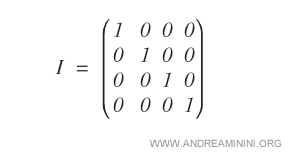
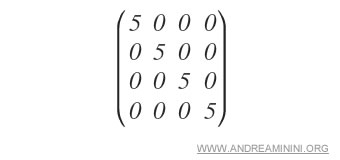
10. Qu’est-ce qu’une matrice scalaire ?
    C’est une matrice carrée dont tous les éléments de la diagonale principale sont identiques et non nuls.
    
11. Qu’est-ce qu’une matrice inversible ?
    Une matrice carrée \( A \) d’ordre \( n \) est inversible s’il existe une matrice \( A^{-1} \) du même ordre telle que \( A \cdot A^{-1} = A^{-1} \cdot A = I_n \).
    
12. Qu’est-ce qu’une matrice orthogonale ?
    C’est une matrice carrée et inversible dont la transposée coïncide avec l’inverse : \( A^T = A^{-1} \).
    
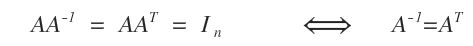
13. Qu’est-ce que le déterminant ?
    C’est un nombre associé à une matrice carrée qui en condense certaines propriétés essentielles. On le note det(A) ou |A|.
    
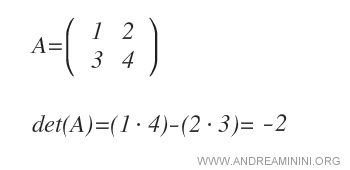
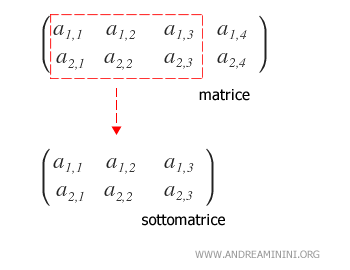
14. Qu’est-ce qu’une sous-matrice ?
    C’est la matrice obtenue en supprimant une ou plusieurs lignes et/ou colonnes d’une matrice donnée.
    
15. Qu’est-ce qu’une sous-matrice complémentaire ?
    C’est une sous-matrice d’ordre inférieur, obtenue en supprimant une seule ligne et une seule colonne de la matrice initiale.
    
16. Qu’est-ce qu’un mineur d’une matrice ?
    C’est le déterminant d’une sous-matrice carrée obtenue en éliminant \( i \) lignes et \( j \) colonnes de la matrice d’origine.
    
17. Qu’est-ce que le mineur complémentaire ?
    C’est le déterminant de la sous-matrice obtenue en supprimant la \( i\)-ème ligne et la \( j\)-ème colonne d’une matrice carrée \( A \).
    
18. Qu’est-ce qu’un cofacteur ?
    Le cofacteur (ou complément algébrique) d’un élément \( a_{ij} \) est le mineur complémentaire associé, multiplié par \( (-1)^{i+j} \).
    
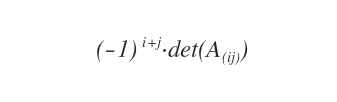
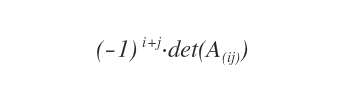
19. Qu’est-ce que la matrice adjointe ?
    C’est la transposée de la matrice des cofacteurs.
    
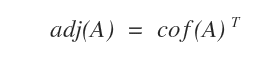
20. Qu’est-ce que la trace d’une matrice ?
    C’est la somme des éléments situés sur la diagonale principale.
    
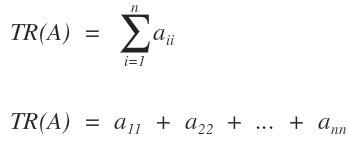
21. Qu’est-ce que le rang d’une matrice ?
    C’est le plus grand ordre des mineurs non nuls que l’on peut extraire de la matrice.
22. Qu’est-ce qu’une matrice singulière ?
    C’est une matrice carrée dont le déterminant est nul et qui, par conséquent, n’est pas inversible.
23. Que sont des matrices semblables ?
    Deux matrices \( A \) et \( B \) sont semblables s’il existe une matrice inversible \( M \) telle que \( M^{-1}AM = B \).