Matrice orthogonale

On dit qu’une matrice A est orthogonale lorsque son inverse, A^-1, coïncide exactement avec sa transposée, A^T.

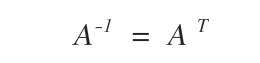
L’ensemble de toutes les matrices orthogonales de dimension n se note O_n.

Remarque. Seules les matrices inversibles peuvent être orthogonales. Ainsi, les matrices orthogonales forment un sous-ensemble de O_n à l’intérieur du groupe GL_n(ℝ), qui rassemble toutes les matrices carrées inversibles d’ordre n.

Une propriété fondamentale des matrices orthogonales est que le produit de A par sa transposée A^T est toujours égal à la matrice identité I_n.

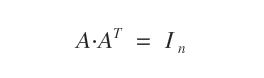
Démonstration

La preuve est immédiate : l’une des propriétés essentielles des matrices inversibles affirme que

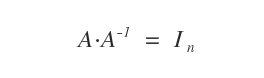
Or, pour une matrice orthogonale, on a A^-1 = A^T. Par conséquent :

$$ AA^T = I_n $$

Exemple concret

Considérons la matrice carrée suivante : elle constitue un exemple typique de matrice orthogonale.

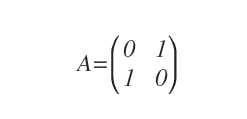
Pour s’en assurer, il suffit de calculer le produit de A par sa transposée A^T.

 

On obtient alors que A · A^T est exactement la matrice identité I₂.

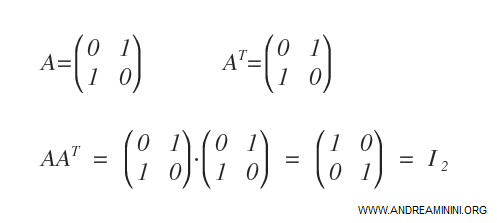
On en conclut que A^T = A^-1.

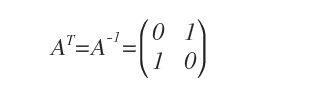
Pourquoi ? Parce qu’une propriété générale des matrices inversibles énonce que le produit d’une matrice A par son inverse A^-1 donne toujours la matrice identité I. Ainsi, si l’on a à la fois AA^T = I et AA^-1 = I, il en découle nécessairement que A^T = A^-1.

Cela établit clairement que A est bien une matrice orthogonale.

Les groupes orthogonaux O et SO

Les matrices orthogonales ne sont pas de simples outils de calcul. Elles constituent une structure mathématique à part entière, appelée groupe orthogonal, notée \( O(n) \). Ce groupe obéit aux quatre règles fondamentales de l’algèbre abstraite qui définissent ce qu’est un groupe au sens mathématique du terme :

1. Clôture : le produit de deux matrices orthogonales est toujours une matrice orthogonale ;
2. Associativité : la multiplication matricielle reste associative ;
3. Élément neutre : la matrice identité \( I \) appartient à \( O(n) \) et joue le rôle d’élément neutre ;
4. Élément inverse : chaque matrice orthogonale \( A \) possède pour inverse sa transposée \( A^{T} \), elle-même orthogonale.

En d’autres termes, l’ensemble des matrices réelles \( A \) qui satisfont

$$ A^{T}A = AA^{T} = I $$

forme un groupe pour la multiplication des matrices.

Le groupe orthogonal \( O(n) \) décrit toutes les isométries linéaires de l’espace euclidien, c’est-à-dire les transformations qui préservent les distances et les angles. Il regroupe notamment les rotations et les réflexions.

Exemple. Dans le plan, une matrice du groupe \( O(2) \) peut représenter une rotation ou une réflexion. Dans l’espace tridimensionnel, les matrices de \( O(3) \) décrivent toutes les rotations et symétries spatiales qui conservent la forme géométrique de l’espace.

En résumé, le groupe \( O(n) \) rassemble toutes les rotations et réflexions possibles dans un espace à \( n \) dimensions.

Cependant, toutes ces transformations ne préservent pas l’orientation de l’espace. Les réflexions, par exemple, l’inversent.

Pour distinguer les transformations qui conservent l’orientation de celles qui l’inversent, on définit à l’intérieur de \( O(n) \) un sous-groupe très important : le groupe orthogonal spécial \( SO(n) \). Il réunit toutes les matrices orthogonales dont le déterminant vaut +1 :

$$ SO(n) = \{ A \in O(n) \;|\; \det(A) = +1 \} $$

Les matrices de \( SO(n) \) correspondent aux rotations pures, qui conservent à la fois les distances, les angles et l’orientation de l’espace.

À l’inverse, les matrices dont le déterminant est -1 représentent les réflexions, qui inversent cette orientation.

Remarque. Cette distinction joue un rôle essentiel en géométrie comme en physique. Le groupe \( SO(3) \) décrit l’ensemble des rotations possibles dans l’espace tridimensionnel, tandis que \( SO(2) \) correspond aux rotations du plan.