Les groupes en mathématiques

Qu’est-ce qu’un groupe ?

Un groupe est une structure algébrique (G,*) formée de deux éléments essentiels :
• un ensemble non vide (G ≠ Ø),
• et une opération binaire $$ *: G \times G \rightarrow G $$ qui obéit à trois règles fondamentales :
  1. Associativité : $$ (a*b)*c = a*(b*c) $$
  2. Élément neutre : il existe un élément e tel que $$ a*e = e*a = a \ \ \forall a \in G $$
  3. Élément inverse : chaque élément a possède un inverse $$ a*(a)^{-1} = (a)^{-1}*a = e $$

En termes simples, un groupe est un monoïde dans lequel chaque élément peut être « annulé » par un autre. C’est une idée à la fois simple et d’une puissance incroyable en mathématiques.

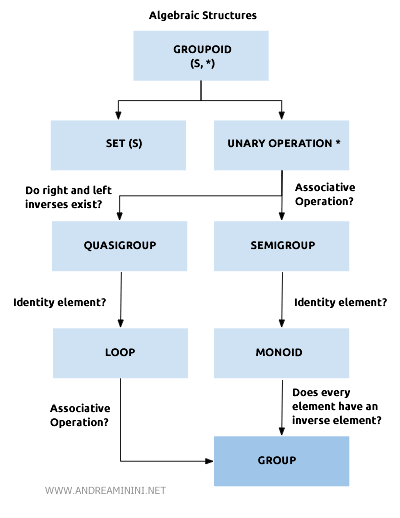
Le nombre d’éléments d’un groupe, noté |G|, s’appelle son ordre.

On distingue deux grands types :

• Groupes finis : ils contiennent un nombre limité d’éléments.
• Groupes infinis : ils comportent une infinité d’éléments.

Les groupes sont au cœur de la théorie des groupes, l’une des branches les plus fondamentales de l’algèbre moderne. Derrière ce concept abstrait se cache l’idée de symétrie - une notion centrale autant en mathématiques qu’en physique, chimie ou informatique.

Exemples simples pour comprendre

Exemple 1 : Les entiers (ℤ) avec l’addition (+)

• La somme de deux entiers est toujours un entier : $$ a+b=c \in \mathbb{Z} $$
• L’addition est associative : $$ (a+b)+c = a+(b+c) $$
• Le zéro joue le rôle d’élément neutre : $$ a+0 = 0+a = a $$
• Chaque nombre a un inverse additif : $$ a+(-a)=(-a)+a=0 $$

Donc, (ℤ, +) est un groupe additif.

Exemple 2 : Les entiers (ℤ) avec la multiplication (·) ne forment pas un groupe, car tous les entiers n’ont pas d’inverse multiplicatif.

Par exemple, l’inverse de 2 serait 1/2, mais 1/2 n’appartient pas à ℤ : $$ 2 \cdot \frac{1}{2} = 1 $$

À retenir : Même si ℤ avec la multiplication vérifie certaines propriétés (fermeture, associativité, existence d’un neutre), il manque les inverses. C’est pourquoi ℤ n’est pas un groupe multiplicatif.

Un peu d’histoire

La théorie des groupes est née au XIXᵉ siècle, quand les mathématiciens se demandaient s’il était possible de résoudre toutes les équations algébriques par des formules générales.

Les travaux de Ruffini, Abel et surtout de Évariste Galois ont montré que non : certaines équations sont « indomptables », et leur résolubilité dépend des propriétés d’un groupe sous-jacent. C’est une idée révolutionnaire, qui allait donner naissance à l’algèbre moderne.

En 1854, Arthur Cayley formula la première définition abstraite d’un groupe, indépendante des équations. Puis, au XXᵉ siècle, Emmy Noether en perfectionna la formulation et étendit le concept aux groupes finis et infinis.

Aujourd’hui, la théorie des groupes est partout : dans la géométrie, la physique des particules, la cristallographie, la théorie des nombres et même la cryptographie.

Les groupes abéliens

Un groupe est abélien (ou commutatif) si l’ordre des opérations n’a pas d’importance : $$ a*b = b*a $$

Exemple : Les nombres rationnels (ℚ) avec l’addition (+).

• $$ (a+b)+c = a+(b+c) $$
• $$ a+0=0+a=a $$
• $$ a+(-a)=(-a)+a=0 $$
• $$ a+b=b+a $$

Ce sont toutes les propriétés d’un groupe abélien.

Remarque : En excluant le zéro, les rationnels forment aussi un groupe abélien pour la multiplication (ℚ,*) : 1 est l’élément neutre, et chaque a a pour inverse son réciproque 1/a.

Les groupes non abéliens

Un groupe est non abélien quand l’ordre des opérations change le résultat.

Les groupes symétriques et groupes diédraux en sont des exemples classiques.

Exemple : La multiplication des matrices n’est pas commutative.

En effet : $$ A \cdot B \ne B \cdot A $$

Le produit se calcule en multipliant les lignes de la première matrice par les colonnes de la seconde.

Remarque : En revanche, l’ensemble des matrices (M,+) forme un groupe abélien pour l’addition. L’ordre d’addition n’a aucune influence sur le résultat.

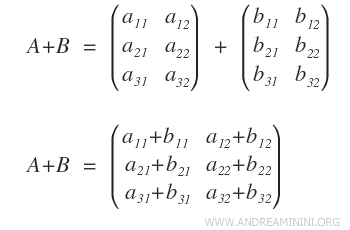
La table de multiplication

Quand un groupe est composé d’un petit nombre d’éléments, on peut représenter son fonctionnement à l’aide d’une table de multiplication.

Chaque ligne et chaque colonne correspondent à un élément du groupe, et chaque cellule indique le résultat de leur combinaison.

	a	b	...	z
a	a*a	a*b	...	a*z
b	b*a	b*b	...	b*z
...
z	z*a	z*b	...	z*z

Cette représentation visuelle aide à mieux comprendre la structure interne d’un groupe et la logique de son opération.

Exemple concret : le groupe modulo 8

Pour mieux comprendre ce qu'est un groupe, prenons un exemple simple : le groupe S composé des éléments { 0,1,2,3,4,5,6,7 }, muni de l'addition modulo 8.

Qu'est-ce que l'addition modulo 8 ? C'est une opération typique de l'arithmétique modulaire, aussi appelée « arithmétique du cadran » ou « de l'horloge ». Ici, lorsqu'une somme dépasse 7, on revient à 0 comme si le calcul se faisait sur un cercle. Par exemple : 5+2=7, 6+2=0, 7+2=1, etc. C'est une addition qui "tourne en boucle".

Voici la table de composition du groupe (S,+₈) :

a+b	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7	0
2	2	3	4	5	6	7	0	1
3	3	4	5	6	7	0	1	2
4	4	5	6	7	0	1	2	3
5	5	6	7	0	1	2	3	4
6	6	7	0	1	2	3	4	5
7	7	0	1	2	3	4	5	6

Ce système respecte les trois conditions d'un groupe :

• Associativité : $$ 1+(2+3) = (1+2)+3 = 6 $$
• Élément neutre : le zéro ne change rien au résultat : $$ 1+0=1, \ 2+0=2, \dots $$
• Inverse additif : chaque nombre a un "opposé" qui ramène à zéro : $$ 1+7=0, \ 2+6=0, \ 3+5=0, \ 4+4=0, \dots $$

Ordre d'un groupe

L'ordre d'un groupe est simplement le nombre d'éléments qu'il contient. On le note $$ |G| $$ et c'est une donnée essentielle pour en comprendre la structure.

Exemple : dans notre groupe S, il y a huit éléments, donc :

$$ |S| = 8 $$

Ordre d'un élément

L'ordre d'un élément g est le plus petit entier positif h pour lequel répéter h fois l'opération sur g ramène à l'élément neutre e :

$$ g^h = e $$

Si ce h n'existe pas, on dit que g est d'ordre infini.

Quand l'ordre est fini, l'ensemble des puissances de g forme le sous-groupe engendré par g, noté <g> :

$$ <g> = \{ e, g, g^2, ..., g^{h-1} \} $$

Exemple : dans le groupe (S, +₈), les ordres des éléments sont :

Élément	Ordre	Calcul
0	1	01 = 0
1	8	18 = 0
2	4	24 = 2+2+2+2 = 0
3	8	38 = 3×8 = 0 (mod 8)
4	2	42 = 4+4 = 0
5	8	58 = 0
6	4	64 = 6+6+6+6 = 0
7	8	78 = 0

L'ordre d'un élément correspond à la taille du sous-groupe qu'il génère.

Exemple : L'élément 2 a un ordre de 4. Le sous-groupe qu'il engendre est :

$$ <2> = \{ 2, 4, 6, 0 \} $$

Ce sous-groupe contient quatre éléments, tout comme l'ordre de 2.

Puissances dans un groupe

En théorie des groupes, élever un élément à une puissance ne signifie pas le multiplier "au sens arithmétique", mais répéter l'opération du groupe.

On définit :

$$ g^n = g * g * \dots * g \quad (n \text{ fois}) $$

Exemple : $$ g^4 = g * g * g * g $$

Remarque : Le symbole * dépend du groupe : - dans un groupe additif : $$ g^4 = g + g + g + g $$ - dans un groupe multiplicatif : $$ g^4 = g * g * g * g $$

Pour les puissances négatives :

$$ g^{-4} = g^{-1} * g^{-1} * g^{-1} * g^{-1} $$

Et par convention :

$$ g^0 = e $$

Note : Dans un groupe additif, $$ g^0 = 0 $$ ; dans un groupe multiplicatif, $$ g^0 = 1 $$.

Les groupes cycliques

Un groupe cyclique est un groupe où un seul élément, appelé générateur, permet d'obtenir tous les autres par répétition de l'opération du groupe.

Autrement dit, si <g> = G, alors le groupe est cyclique.

Exemple : Dans l'arithmétique modulaire de base 8, avec l'addition :

$$ G = (\{0,1,2,3,4,5,6,7\}, +) $$

L'élément 1 suffit pour engendrer tout le groupe :

$$ <1> = \{1,2,3,4,5,6,7,0\} = G $$

G est donc un groupe cyclique d'ordre 8.

Propriétés intéressantes

• Tout groupe cyclique est abélien (l'ordre des opérations n'a pas d'importance).
• Tous ses sous-groupes sont eux aussi cycliques.
• L'ordre de chaque sous-groupe divise celui du groupe.
• Pour chaque diviseur de l'ordre, il existe un unique sous-groupe associé.

Et quand le groupe est infini ?

Un sous-groupe cyclique infini est engendré par un élément dont l'ordre est infini - autrement dit, en le "répétant" on ne retombe jamais sur le point de départ. C'est le cas, par exemple, des entiers (ℤ, +), engendrés par 1 ou -1.