Groupes symétriques

Un groupe symétrique \( (S_n, *) \) défini sur un ensemble \( S \) est constitué de toutes les permutations possibles des éléments de \( S \), c'est-à-dire de toutes les façons de réorganiser ces éléments. L'opération du groupe est la composition des applications : \( f * g = f \circ g = f[g] \).

Autrement dit, chaque permutation est une application bijective \( \sigma \) qui associe à chaque élément de \( S \) un unique élément du même ensemble :

$$ \sigma : S \rightarrow S $$

L'ensemble de toutes ces bijections forme \( S_n \) :

$$ S_n = \{ \sigma_1, \sigma_2, \dots, \sigma_k \} $$

Le groupe symétrique \( (S_n, *) \) a un ordre égal à \( n! \) (factorielle de \( n \)), car il existe exactement \( n! \) façons différentes de disposer \( n \) éléments.

Remarque : Tous les groupes symétriques d'ensembles finis ayant le même nombre d'éléments sont isomorphes. À partir de \( n > 2 \), ils deviennent non abéliens, c'est-à-dire que la composition n'est plus commutative.

Un exemple concret

Pour bien comprendre, prenons un petit ensemble à trois éléments :

$$ S = \{ 1, 2, 3 \} $$

Le nombre total de permutations possibles est :

$$ n! = 3 \cdot 2 \cdot 1 = 6 $$

Les six permutations de \( S \) forment donc :

$$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$

Choisissons par exemple la permutation :

$$ \sigma : (1, 2, 3) \rightarrow (2, 3, 1) $$

Elle se représente sous forme matricielle :

$$ \sigma = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

Chaque colonne indique comment les éléments de \( S \) sont réarrangés par \( \sigma \).

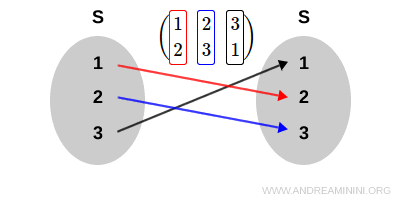
Remarque : L'action de \( \sigma \) est la suivante : $$ \sigma(1) = 2 \\ \sigma(2) = 3 \\ \sigma(3) = 1 $$ Autrement dit, \( 1 \) devient \( 2 \), \( 2 \) devient \( 3 \) et \( 3 \) devient \( 1 \).

Composition de permutations

Toutes les permutations de \( S \) constituent le groupe symétrique \( (S_n, *) \), où l'opération est la composition des applications. Dans notre exemple, ce groupe est d'ordre \( n! = 6 \).

L'opération de composition * combine deux permutations pour en former une nouvelle, toujours dans \( S_n \).

Considérons, par exemple :

$$ \sigma_1 : (1, 2, 3) \rightarrow (2, 1, 3) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$

$$ \sigma_2 : (1, 2, 3) \rightarrow (2, 3, 1) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

La composition de ces deux permutations est :

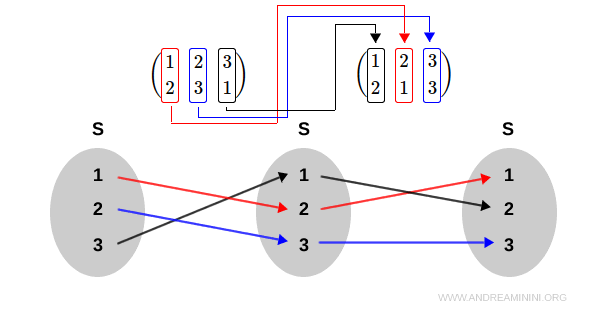
$$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

On procède toujours de droite à gauche : on applique d'abord \( \sigma_2 \), puis \( \sigma_1 \). Le résultat est :

$$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$

Explication pas à pas : - \( \sigma_2(1) = 2 \), \( \sigma_1(2) = 1 \), donc \( \sigma_1 * \sigma_2(1) = 1 \).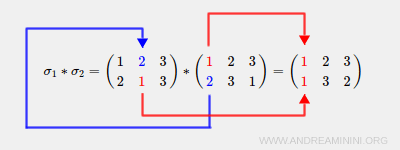
- \( \sigma_2(2) = 3 \), \( \sigma_1(3) = 3 \), donc \( \sigma_1 * \sigma_2(2) = 3 \).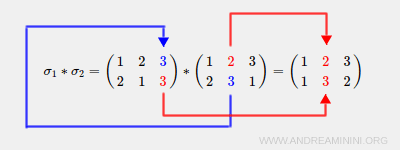
- \( \sigma_2(3) = 1 \), \( \sigma_1(1) = 2 \), donc \( \sigma_1 * \sigma_2(3) = 2 \).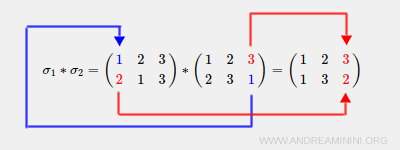

Le groupe est-il abélien ?

Le groupe symétrique \( (S_n, *) \), qui regroupe toutes les permutations de \( n \) éléments, est un exemple classique de groupe non abélien dès que \( n > 2 \). Cela signifie que l'ordre dans lequel on compose les permutations change le résultat.

Vérification : Dans l'exemple précédent : $$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$ Mais si l'on inverse l'ordre : $$ \sigma_2 * \sigma_1 = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ On constate donc que : $$ \sigma_1 * \sigma_2 \ne \sigma_2 * \sigma_1 $$ La composition n'étant pas commutative, le groupe \( (S_n, *) \) est bien un groupe non abélien.

Ce type de groupe joue un rôle fondamental en algèbre, car il permet de modéliser toutes les transformations réversibles d'un ensemble fini. Il constitue aussi la base de nombreuses applications en mathématiques, en physique et en informatique.