Les structures algébriques
Qu’est-ce qu’une structure algébrique ?
Une structure algébrique, c’est tout simplement un ensemble S accompagné d’une ou plusieurs opérations définies sur lui. $$ (S,*) $$
Lorsqu’il n’y a qu’une seule opération, on parle d’un groupoïde.
Si cette opération est associative, c’est-à-dire que l’ordre des calculs n’influence pas le résultat, la structure devient un demi-groupe.
Et si, en plus, il existe un élément qui ne change pas le résultat lorsqu’on l’utilise (comme le zéro pour l’addition ou le un pour la multiplication), alors on parle d’un monoïde.
Mais au fait, qu’est-ce qu’une opération ?
Une opération est une règle qui combine des éléments de l’ensemble S pour en produire un autre, appartenant lui aussi à S.
$$ *: S \rightarrow S $$
Lorsqu’elle agit sur deux éléments à la fois (comme l’addition ou la multiplication), on parle d’une opération binaire.
$$ *: S×S \rightarrow S $$
Des exemples pour mieux comprendre
Exemple 1
Prenons l’ensemble des entiers relatifs Z et l’addition (+) comme opération.
$$ ( Z , + ) $$
Ici, chaque paire d’entiers (les termes) donne un autre entier (la somme). Tout reste dans Z, donc on a bien une structure algébrique.
$$ +: ZxZ \rightarrow Z $$
Remarque : Si le résultat de l’opération sortait de l’ensemble, la structure algébrique serait rompue.
Exemple 2
Considérons maintenant les nombres de 1 à 10, avec la multiplication (*) comme opération.
$$ S = ( 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ) $$
Cette fois, (S,*) ne forme pas une structure algébrique, car certains produits dépassent les limites de S.
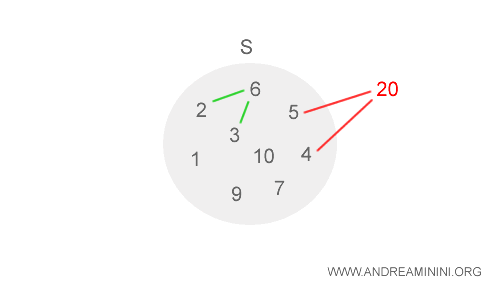
Par exemple, 4×5 = 20, et 20 n’appartient pas à S.
$$ (1*2)=2 \\ (2*3)=6 \\ (4*5)=20 $$
La condition essentielle - que le résultat reste dans l’ensemble - n’est donc pas respectée.
À retenir : un même ensemble peut être une structure algébrique pour une opération donnée, mais pas pour une autre.
Par exemple, les nombres naturels N forment une structure algébrique avec l’addition (N,+), mais pas avec la soustraction (N,-), car soustraire deux naturels peut donner un résultat négatif, qui n’appartient plus à N.
Représenter une structure : la table de vérité
Quand une structure algébrique comporte peu d’éléments, on peut la représenter facilement à l’aide d’une table de vérité - un tableau qui montre le résultat de l’opération pour toutes les combinaisons possibles.
Exemple
Soit l’ensemble S = {a, b, c} et une opération notée |
$$ (S,|) $$
L’opération associe à chaque paire (x,y) un élément de S. Voici la table correspondante :
| a | b | c | |
|---|---|---|---|
| a | a | a | b |
| b | c | b | a |
| c | a | b | c |
Ce tableau illustre une structure algébrique simple, appelée groupoïde, car elle repose sur une seule opération.
Et à partir de là, on peut construire des structures plus complexes !
Remarque importante : la manière de relier les couples d’éléments à leurs résultats n’est pas fixée d’avance. Par exemple, le résultat de (a,b) pourrait être c, a ou b, selon la fonction choisie ou le circuit logique utilisé. L’unique condition pour parler de structure algébrique est que le résultat appartienne toujours à l’ensemble S.