Corps de division (ou corps non commutatif)
Un corps de division est un anneau (S,+,·) doté de deux propriétés essentielles. Il possède un élément neutre pour la multiplication et tout élément non nul y est inversible. Ces deux conditions donnent à la structure un comportement particulièrement riche, surtout lorsque la multiplication n'est pas commutative.
Dans un corps de division, il existe un élément neutre multiplicatif vérifiant:
$$ a \cdot 1 = a \ \ \ \ \ \forall \ a \in R $$
De plus, tout élément non nul admet un inverse multiplicatif:
$$ a \cdot a^{-1} = 1 \ \ \ \ \ \forall \ a \ , \ a \ne 0 \ \ \in R $$
Cela signifie que l'ensemble S muni de la multiplication forme un groupe multiplicatif. Cette structure générale permet de travailler avec des objets où l'on peut toujours diviser par un élément non nul, même lorsque la multiplication ne commute pas.
Nota: Les termes « somme » et « multiplication » ne doivent pas être compris de manière trop restrictive. Dans d'autres cadres algébriques, ils peuvent désigner des opérations de nature différente.
Lorsque la multiplication est commutative, le corps de division devient un corps commutatif, souvent appelé simplement un corps. Dans la grande majorité des situations, ce sont ces corps commutatifs qui interviennent, mais les corps de division non commutatifs jouent un rôle important dans plusieurs domaines avancés, notamment en algèbre et en géométrie.
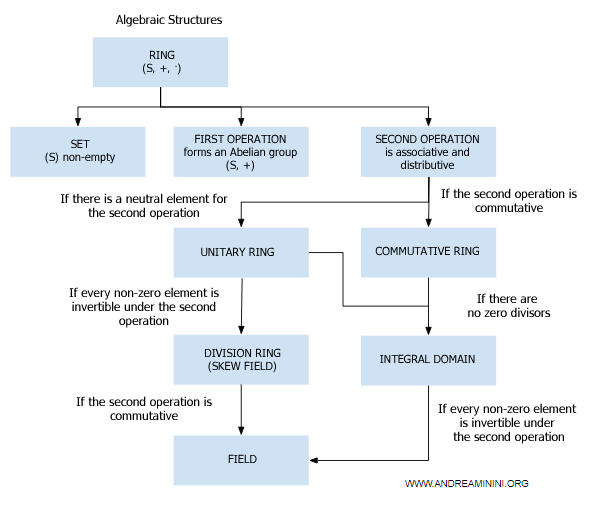
Un exemple concret
Pour mieux comprendre, examinons le cas des nombres réels R, munis de l'addition et de la multiplication habituelles:
$$ (R, + , \cdot ) $$
Pour déterminer si ce système forme un corps de division, il suffit d'examiner le comportement de chacune des deux opérations.
Première opération: l'addition (+)
L'addition des réels présente toutes les propriétés attendues d'un groupe abélien. La somme de deux réels est toujours un réel, l'opération est associative, elle possède un élément neutre (0) et chaque réel a un opposé.
- Fermeture: $$ \forall \ a,b \in R \ \ \ a+b \in R $$
- Associativité: $$ \forall \ a,b,c \in R \ \ \ (a+b)+c = a+(b+c) $$
- Élément neutre: $$ \forall \ a \in R \ \ \ a+0 = a $$
- Inverse additif: $$ \forall \ a \in R \ \ \ a + (-a) = 0 $$
Comme l'addition est commutative, (R,+) est un groupe abélien. Cette première condition est donc entièrement satisfaite.
Deuxième opération: la multiplication (·)
La multiplication sur R remplit elle aussi toutes les propriétés requises. Elle est interne, associative et distributive par rapport à l'addition. Elle possède un élément neutre (1) et tout réel non nul possède un inverse multiplicatif.
- Fermeture: $$ \forall \ a,b \in R \ \ \ a \cdot b \in R $$
- Distributivité: $$ \forall \ a,b,c \in R \ \ \ a \cdot (b+c) = ab + ac $$ $$ \forall \ a,b,c \in R \ \ \ (a+b) \cdot c = ac + bc $$
- Associativité: $$ \forall \ a,b,c \in R \ \ \ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
- Élément neutre: $$ \forall \ a \in R \ \ \ a \cdot 1 = a $$
- Inverse multiplicatif: $$ \forall \ a\ne 0 \ \ \ a \cdot a^{-1} = 1 $$
Les deux opérations satisfont donc pleinement les propriétés nécessaires. L'anneau (R,+,·) est bien un corps de division.
Nota: Dans l'exemple des réels, la multiplication est commutative. On obtient donc en réalité un corps au sens usuel du terme.
Et ainsi de suite.