Semi-groupes

Qu’est-ce qu’un semi-groupe ?

Un semi-groupe est une structure algébrique (S, *) constituée d’un ensemble S muni d’une opération binaire fermée S×S→S, appelée opération de composition. Cette opération satisfait à la propriété associative, c’est-à-dire : $$ (a * b) * c = a * (b * c) \ \ \ \forall \ a, b, c \ \in S $$

On le désigne également sous le nom de pseudo-groupe.

Un semi-groupe ne nécessite ni élément neutre, ni élément inverse.

Lorsqu’un élément neutre est présent, le semi-groupe devient un monoïde.

Exemple

Considérons l’ensemble des nombres naturels N muni de l’opération d’addition +.

$$ (N, +) $$

Cette structure constitue un groupoïde, car elle repose sur une opération binaire interne.

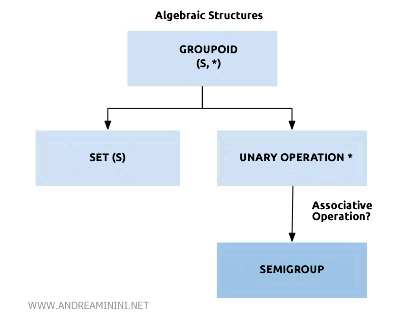
Elle forme en outre un semi-groupe, puisque l’addition est associative.

Pour tout triplet de nombres naturels a, b et c, l’addition vérifie bien l’associativité :

$$ a + (b + c) = (a + b) + c $$

Par exemple, si a = 2, b = 3, c = 4 :

$$ 2 + (3 + 4) = (2 + 3) + 4 = 9 $$

Et ainsi de suite.