Les anneaux en algèbre abstraite
En algèbre abstraite, un anneau (R,+,·) est une structure algébrique formée d'un ensemble R muni de deux opérations binaires : l'addition et la multiplication. Ces deux opérations sont dites fermées, car le résultat appartient toujours à R : $$ R \times R \rightarrow R $$
Pour que (R,+,·) soit un anneau, ces opérations doivent satisfaire un ensemble précis de propriétés.
Addition
L'addition doit vérifier quatre propriétés fondamentales :
- Commutativité
$$ a+b = b+a \ \ \ \forall \ a,b \in R $$ - Associativité
$$ (a+b)+c = a+(b+c) \ \ \ \forall \ a,b,c \in R $$ - Existence d'un élément neutre
$$ a+0 = 0+a = a \ \ \ \forall \ a \in R $$ - Existence d'un inverse additif
$$ a+(-a) = 0 \ \ \ \forall \ a \in R $$
Multiplication
La multiplication doit quant à elle respecter deux règles essentielles :
- Associativité
$$ (a \cdot b) \cdot c = a \cdot (b \cdot c) \ \ \ \forall \ a,b,c \in R $$ - Distributivité
$$ a \cdot (b+c) = a \cdot b + a \cdot c \ \ \ \forall \ a,b,c \in R $$ $$ (a + b) \cdot c = a \cdot c + b \cdot c \ \ \ \forall \ a,b,c \in R $$
Dans cette présentation, on se réfère souvent à l'ensemble des nombres réels R pour simplifier les exemples, mais en réalité, tout ensemble peut convenir.
Les deux opérations n'ont pas le même statut. L'addition doit toujours former un groupe abélien, c'est-à-dire une structure parfaitement symétrique, alors que la multiplication peut être plus libre.
Remarque : Dans un anneau, l'addition est toujours commutative et possède un élément neutre ainsi que des inverses. La multiplication, elle, n'est pas forcément commutative et peut ne pas avoir d'élément neutre ni d'inverses. L'ordre des opérations est fondamental : (R,+,·) est un anneau, mais (R,·,+) ne l'est pas, car zéro n'a pas d'inverse multiplicatif. En résumé, (R,+) est un groupe abélien, tandis que (R,·) n'est en général qu'un semi-groupe.
Par convention, on parle d'« addition » et de « multiplication », mais ces opérations peuvent représenter toute paire d'opérations vérifiant les mêmes axiomes.
Un exemple concret
Un bon exemple d'anneau est l'ensemble des matrices carrées Mn(Z) d'ordre n, c'est-à-dire comportant n lignes et n colonnes, à coefficients entiers. On y définit :
- l'addition élément par élément ;
- la multiplication par le produit ligne par colonne.
Ces deux opérations sont fermées : le résultat d'une addition ou d'une multiplication de deux matrices carrées est toujours une autre matrice carrée du même ordre.
$$ M_n(Z) \times M_n(Z) \rightarrow M_n(Z) $$
Vérification des propriétés
Première opération - L'addition de matrices est commutative et associative, admet la matrice nulle comme élément neutre et chaque matrice possède un inverse additif (son opposée) :
$$ A + (-A) = 0 \ \ \ \forall \ A \in M_n(Z) $$
Ces conditions garantissent que (Mn(Z),+) forme un groupe abélien.
Seconde opération - La multiplication matricielle est associative et distributive par rapport à l'addition :
$$ (A + B) \cdot C = A \cdot C + B \cdot C $$
$$ A \cdot (B + C) = A \cdot B + A \cdot C $$
Elle satisfait donc les conditions exigées pour la multiplication dans un anneau.
Conclusion
Les deux opérations réunissent toutes les propriétés nécessaires. Ainsi, (Mn(Z),+,*) constitue bien un anneau.
Les principaux types d'anneaux
Certains anneaux possèdent des caractéristiques supplémentaires. Voici les plus importants :
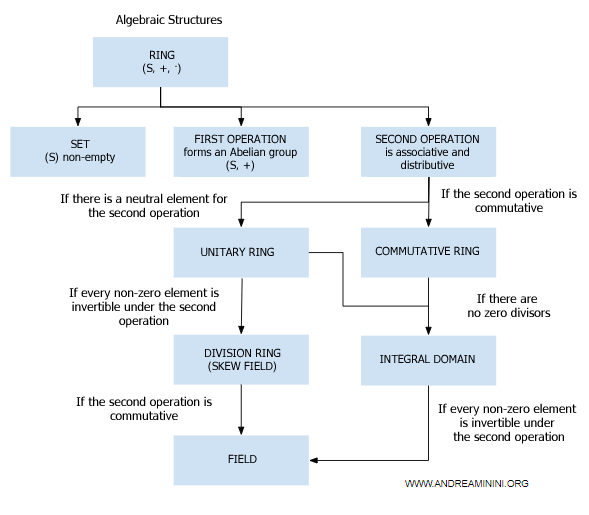
- Anneau commutatif
La multiplication est commutative : $$ a \cdot b = b \cdot a \ \ \forall \ a,b \in R $$ - Anneau unitaire
Il existe un élément neutre pour la multiplication : $$ a \cdot 1 = 1 \cdot a = a \ \ \forall \ a \in R $$ - Domaine intègre
Anneau commutatif et unitaire sans diviseurs de zéro : $$ \forall \ a,b \in R, \ ab = 0 \ \Rightarrow \ a = 0 \ \text{ou} \ b = 0 $$ - Anneau à division
Anneau unitaire dans lequel tout élément non nul possède un inverse multiplicatif : $$ a \cdot a^{-1} = 1 \ \ \forall \ a \neq 0 \in R $$ - Corps
Anneau commutatif et unitaire où chaque élément non nul est inversible : $$ a \cdot a^{-1} = 1 \ \ \forall \ a \neq 0 \in R $$
Ces différentes catégories d'anneaux constituent la base de nombreuses théories en algèbre, de l'arithmétique modulaire à l'algèbre linéaire, et jouent un rôle central dans la compréhension des structures mathématiques modernes.