Isomorphisme d’anneaux
Un isomorphisme entre deux anneaux A et A' est une application bijective $$ \phi: A \rightarrow A' $$ qui conserve les deux opérations fondamentales de l'anneau. Autrement dit, pour tous $a, b \in A$, on a $$ \phi(a + b) = \phi(a) + \phi(b) $$ $$ \phi(a \cdot b) = \phi(a) \cdot \phi(b) $$ L'application respecte donc l'addition et la multiplication, ce qui garantit que la structure algébrique est parfaitement préservée. 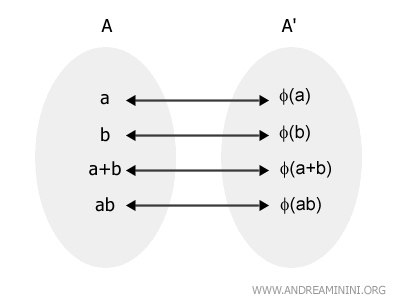
Dans ce cas, les anneaux A et A' sont dits isomorphes:
$$ A \simeq A' $$
Cette relation forme une véritable relation d'équivalence. Elle indique que les deux anneaux possèdent la même structure interne. Ils se comportent de manière identique du point de vue algébrique, même s'ils ne sont pas constitués des mêmes éléments.
On dit alors qu'ils appartiennent à la même classe d'isomorphisme.
Un exemple concret
Pour mieux comprendre, regardons un cas familier: l'anneau des nombres complexes $\mathbb{C}$. Considérons l'application qui associe à chaque nombre complexe $$ z = a + bi $$ son conjugué $z'$:
$$ z' = \operatorname{Re}(z) - \operatorname{Im}(z) \cdot i $$
Cette application est bijective et associe à tout nombre complexe un autre élément de $\mathbb{C}$. Elle définit donc un automorphisme, c'est-à-dire un isomorphisme de l'anneau sur lui-même.
Voyons cela en pratique avec deux nombres:
$$ z_1 = 3 + 4i $$
$$ z_2 = 5 - 2i $$
Leurs conjugués sont:
$$ z'_1 = 3 - 4i $$
$$ z'_2 = 5 + 2i $$
Et on peut retrouver les valeurs initiales sans aucune ambiguïté:
$$ z_1 = 3 + 4i $$
$$ z_2 = 5 - 2i $$
Compatibilité avec l'addition
La conjugaison respecte la somme:
$$ z_1 + z_2 = (3 + 4i) + (5 - 2i) = 8 + 2i $$
$$ (z_1 + z_2)' = 8 - 2i $$
Et l'on reconstruit bien la valeur initiale:
$$ z_1 + z_2 = 8 + 2i $$
Compatibilité avec le produit
Elle respecte aussi le produit:
$$ z_1 \cdot z_2 = (3 + 4i)(5 - 2i) = 23 + 14i $$
$$ (z_1 \cdot z_2)' = 23 - 14i $$
Ce qui permet à nouveau de retrouver la valeur d'origine:
$$ 23 + 14i $$
Grâce à ces vérifications, on voit clairement que la conjugaison définit un automorphisme de l'anneau $\mathbb{C}$. C'est un exemple simple mais très parlant de la manière dont un isomorphisme préserve entièrement la structure d'un anneau.