Domaines d’intégrité
Un domaine d'intégrité est un anneau (S, +, ·) commutatif et unitaire dans lequel aucun produit de deux éléments non nuls n'est égal à zéro. Autrement dit : $$ \forall \ a, b \in S \ , \ ab = 0 \Rightarrow (a = 0 \ \text{ou}\ b = 0) $$
En clair, dans un domaine d'intégrité, le produit de deux éléments ne peut s'annuler que si l'un des deux est nul. Ce type de structure joue un rôle central en algèbre, notamment dans l'étude des corps et des extensions de corps.
Pour vérifier qu'un anneau (S, +, ·) est un domaine d'intégrité, il suffit donc de montrer qu'il ne contient aucun diviseur de zéro.
Diviseur de zéro : dans un anneau commutatif (S, +, ·), un élément non nul a ≠ 0 est appelé diviseur de zéro s'il existe un autre élément non nul b ≠ 0 tel que ab = 0.
Exemple 1 : les entiers relatifs
L'ensemble des entiers relatifs Z, muni des opérations d'addition et de multiplication usuelles, forme un anneau commutatif :
$$ (Z,+,\cdot) $$
Le produit de deux entiers non nuls n'est jamais nul :
$$ \forall a,b \in Z, \ a \ne 0, \ b \ne 0 \ \Longrightarrow \ ab \ne 0 $$
Remarque. Si les deux entiers ont le même signe, leur produit est positif. S'ils ont des signes contraires, leur produit est négatif. Dans tous les cas, le produit ne peut être nul que si l'un des deux facteurs l'est : $$ a \cdot 0 = 0 \cdot a = 0 $$
On en conclut que Z ne contient aucun diviseur de zéro. Par conséquent, (Z, +, ·) est un domaine d'intégrité.
Exemple 2 : l'anneau des entiers modulo 6
Considérons maintenant l'ensemble des classes de résidus modulo 6 :
$$ Z_6 = \{ 0,1,2,3,4,5 \} $$
Dans cet anneau commutatif (Z6, +, ·), la multiplication et l'addition sont définies modulo 6 :
$$ (Z_6,+, \cdot) $$
Pour savoir si Z6 contient des diviseurs de zéro, observons sa table de multiplication :
| a ·6 b | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
On remarque ici plusieurs produits nuls entre éléments non nuls : par exemple, 2⋅3 ≡ 0 (mod 6), 3⋅4 ≡ 0, etc. Les nombres 2, 3 et 4 sont donc des diviseurs de zéro.
Calculons explicitement : $$ 2 \cdot 3 = 6 $$ et comme $$ 6 \div 6 = 1 \ \text{reste} = 0 $$ le reste est nul, donc $$ 2 \cdot 3 \equiv 0 \ (\text{mod } 6) $$. On a donc un produit nul entre deux éléments non nuls.
Conclusion : (Z6, +, ·) n'est pas un domaine d'intégrité. En effet, la présence de diviseurs de zéro empêche cette propriété.
De façon générale, un anneau Zn est un domaine d'intégrité si et seulement si n est un nombre premier.
Exemple 3 : l'anneau des entiers modulo 7
Considérons maintenant l'ensemble :
$$ Z_7 = \{ 0,1,2,3,4,5,6 \} $$
Le nombre 7 étant premier, les propriétés changent radicalement. L'anneau (Z7, +, ·) défini modulo 7 ne présente aucun diviseur de zéro. Chaque élément non nul y possède un inverse multiplicatif.
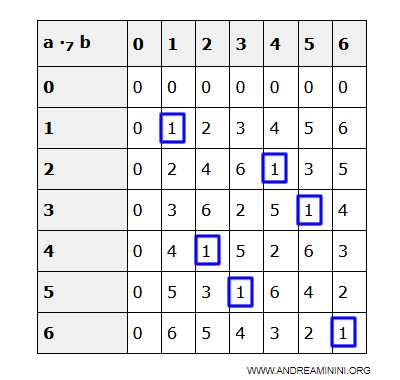
La table de multiplication le confirme :
| a ·7 b | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 0 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
Aucun produit nul entre éléments non nuls : Z7 est donc un domaine d'intégrité.
Pourquoi c'est important
Les domaines d'intégrité sont essentiels en algèbre car ils servent de base à la définition des corps. Lorsqu'un domaine d'intégrité possède la propriété supplémentaire selon laquelle tout élément non nul admet un inverse multiplicatif, il devient un corps.
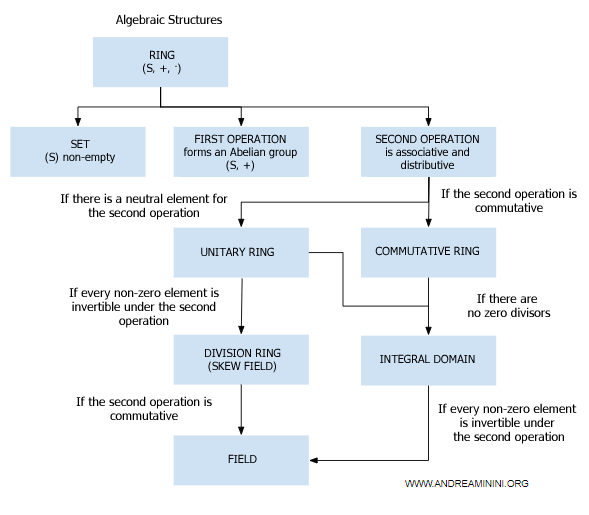
Tout domaine d'intégrité fini est un corps
Un domaine d’intégrité fini devient un corps dès lors que chacun de ses éléments non nuls est inversible pour la multiplication.
Démonstration. Soit (D, +, ·) un domaine d’intégrité fini contenant n éléments : $$ D = \{ a_1, a_2, ..., a_n \} $$ Tous ces éléments sont distincts.
Exemple. Considérons l’ensemble Z7 : $$ D = \{ 0,1,2,3,4,5,6 \} $$ qui est un domaine d’intégrité (Z7, +, ·).
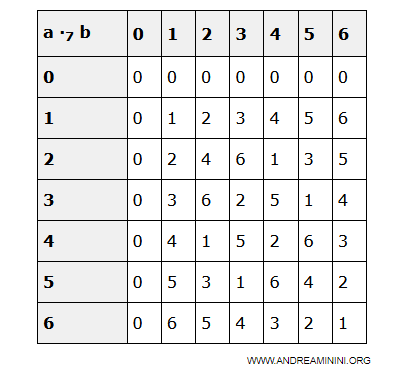
Soit un élément non nul ak de D, $$ a_k \ne 0 $$ et considérons l’application $$ f: a_i \mapsto a_k \cdot a_i $$ Comme D est un domaine d’intégrité, tous les produits ak·ai sont distincts, donc f est injective. D étant fini, f est également surjective.
Exemple. Si l’on choisit ak = 5 dans Z7, les produits de 5 avec les éléments de Z7 sont tous distincts :
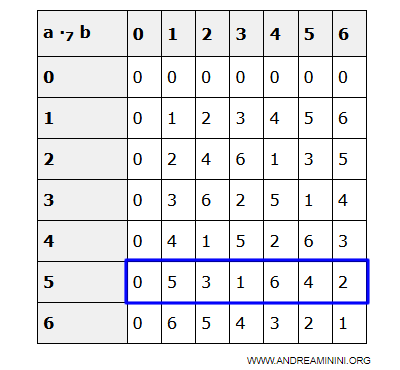
Il existe donc un élément a0 dans D tel que $$ a_k \cdot a_0 = 1 $$ autrement dit, ak est inversible.
Exemple. Dans Z7, si ak = 5, alors a0 = 3 car $$ 5 \cdot 3 = 1 $$.
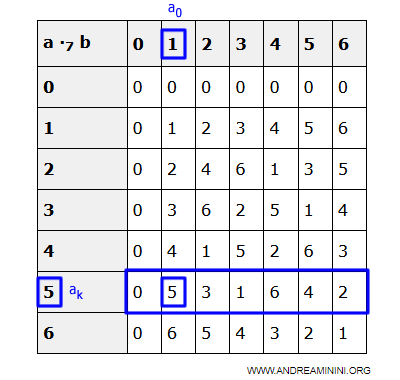
Tout élément x de D peut ainsi s’écrire $$ x = a_k \cdot a_i $$
Exemple. En observant la table de multiplication de Z7, on voit que l’élément 5 engendre tous les éléments de Z7 par multiplication :
$$ 5 \cdot 0 = 0 \\ 5 \cdot 1 = 5 \\ 5 \cdot 2 = 3 \\ 5 \cdot 3 = 1 \\ 5 \cdot 4 = 6 \\ 5 \cdot 5 = 4 \\ 5 \cdot 6 = 2 $$
Comme $$ x = a_0 \cdot x $$ et que la multiplication dans D est associative et commutative, on obtient $$ a_0 = 1 $$, l’élément neutre pour la multiplication dans D.
On a donc démontré l’existence d’un élément neutre et d’inverses multiplicatifs dans D.
Exemple. Dans Z7, tous les éléments non nuls sont inversibles : l’inverse de 1 est 1, celui de 2 est 4, celui de 3 est 5, celui de 4 est 2, celui de 5 est 3 et celui de 6 est 6.
On conclut que le domaine d’intégrité (D, +, ·) est un corps.