Corps en algèbre

En algèbre, un corps est l’une des structures fondamentales. Il s’agit d’un ensemble non vide K, muni de deux opérations internes, l’addition et la multiplication, notées + et ·. On écrit cette structure $$ (\ K \ , \ + \ , \ \cdot \ ) $$. Pour dire qu’un ensemble est un corps, ces opérations doivent vérifier un ensemble précis de règles.

1. Commutativité $$ x+y=y+x $$ $$ x\cdot y=y\cdot x $$
2. Associativité $$ (x+y)+z = x+(y+z) $$ $$ (x\cdot y)\cdot z = x\cdot(y\cdot z) $$
3. Distributivité $$ (x+y)\cdot z = x\cdot z + y\cdot z $$ $$ x\cdot(y+z) = x\cdot y + x\cdot z $$
4. Élément neutre additif Un élément 0 tel que $$ 0+x = x+0 = x $$
5. Élément neutre multiplicatif Un élément 1 tel que $$ 1\cdot x = x\cdot 1 = x $$
6. Inverse additif Pour chaque x, un opposé -x vérifiant $$ x + (-x) = 0 $$
7. Inverse multiplicatif Pour tout x non nul, un inverse \(x^{-1}\) vérifiant $$ x\cdot x^{-1} = 1 $$

Remarque. Dans la théorie algébrique, un corps peut être considéré comme un anneau dans lequel la multiplication est commutative et où tout élément non nul possède un inverse.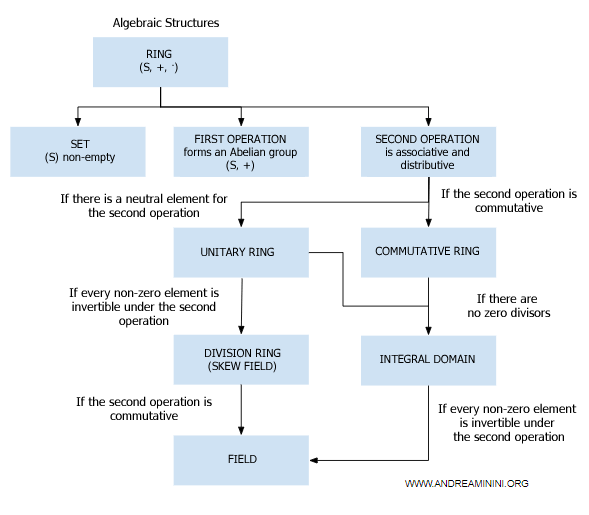

Lorsqu’un corps est constitué uniquement de nombres, on parle de corps numérique (ou corps de nombres). C’est un cas particulier d’un corps général, qui peut tout aussi bien être formé de polynômes, de fonctions ou d’autres objets algébriques.

Un exemple concret

Un exemple classique de corps est celui des nombres rationnels Q, muni de l’addition et de la multiplication usuelles:

$$ (Q, + , \cdot ) $$

Pour montrer que Q est un corps, on vérifie successivement les propriétés des deux opérations.

Addition

L’addition dans Q satisfait les propriétés essentielles:

• Fermeture: si a et b sont rationnels, a+b l’est aussi.
• Associativité: $$ (a+b)+c = a+(b+c) $$
• Présence d’un neutre: $$ a+0 = a $$
• Inverse additif: $$ a + (-a) = 0 $$

De plus, l’addition y est commutative:

$$ a+b = b+a $$

On obtient ainsi un groupe abélien (Q,+), ce qui constitue la première partie des axiomes d’un corps.

Multiplication

La multiplication vérifie également toutes les propriétés nécessaires:

• Fermeture: $$ a\cdot b \in Q $$
• Distributivité: $$ a\cdot(b+c)=ab+ac $$ $$ (a+b)\cdot c = ac+bc $$
• Associativité: $$ (a\cdot b)\cdot c = a\cdot(b\cdot c) $$
• Neutre multiplicatif: $$ a\cdot 1 = a $$
• Inverse pour tout rationnel non nul: $$ a\cdot a^{-1} = 1 $$

La multiplication est elle aussi commutative:

$$ a\cdot b = b\cdot a $$

On conclut alors que (Q,+,·) est bien un corps.

Corps commutatifs

Un corps est dit commutatif lorsque l’ordre des termes ne change jamais le résultat des opérations. Dans la pratique, la quasi-totalité des corps étudiés en mathématiques sont commutatifs, et le mot « corps » est souvent employé directement dans ce sens.

Exemple

Dans le corps des nombres réels, on retrouve les propriétés usuelles:

$$ 3 + 4 = 4 + 3 $$

$$ 2 \cdot 5 = 5 \cdot 2 $$

Notes supplémentaires

• Corps et anneau de division
  Un corps peut être décrit comme un anneau de division où la multiplication est commutative. Tout élément non nul y possède un inverse, ce qui n’est pas le cas dans des structures comme les quaternions, où la multiplication n’est pas commutative.
• Corps numérique et corps général
  Un corps numérique est un cas particulier de corps contenant uniquement des nombres. À l’inverse, un corps général peut être constitué d’objets mathématiques variés. Tout corps numérique est un corps, mais l’inverse n’est pas toujours vrai.

Cette structure joue un rôle central dans l’algèbre moderne, l’arithmétique, la géométrie et de nombreuses théories plus avancées.