Groupoïdes

Qu'est-ce qu'un groupoïde ?

Un groupoïde (ou magma) est une structure algébrique définie par un ensemble non vide S muni d'une opération binaire fermée S×S→S.

En algèbre abstraite, le groupoïde constitue la structure de base à partir de laquelle l'on construit toutes les autres structures algébriques.

En introduisant des axiomes supplémentaires, on fait émerger diverses structures algébriques dérivées du groupoïde.

Remarque : lorsque l'opération du groupoïde est l'addition, on parle de groupoïde additif (S,+) ; lorsqu'il s'agit de la multiplication, on parle de groupoïde multiplicatif (S,*).

Si l'opération du groupoïde vérifie en outre la propriété associative, on obtient alors ce que l'on appelle un pseudo-groupe ou un semi-groupe.

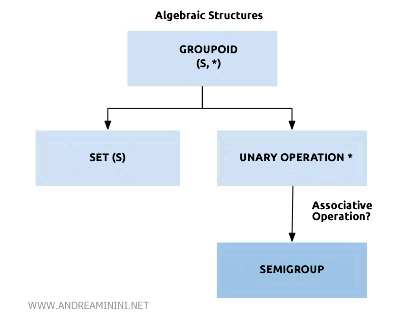
Si chaque élément admet en plus un élément inverse, on parle alors de quasi-groupe.

Un exemple concret

Exemple 1

La structure (N,+) fournit un exemple de groupoïde.

Elle est constituée de l'ensemble des nombres naturels N, muni de l'opération d'addition (+).

Pour tout couple d'éléments de N, leur somme appartient encore à N :

$$ a+b \ \in N \ \ \ \ \ \ \forall \ a,b \in N $$

L'addition (+) est donc bien une opération fermée sur l'ensemble des naturels N.

Remarque : un autre exemple de groupoïde est la structure (N,*), où la multiplication constitue elle aussi une opération fermée sur N.

Exemple 2

La structure (N,-) ne constitue pas un groupoïde, car la soustraction n'est pas une opération fermée sur l'ensemble des nombres naturels.

Par exemple :

$$ 4 - 5 = -1 \notin N $$

Remarque : en revanche, la structure (Z,-), sur l'ensemble des entiers relatifs Z, forme bien un groupoïde, puisque la soustraction y est une opération fermée.

Et ainsi de suite.