Les boucles en algèbre abstraite
Une boucle (ou loop en anglais) est un cas particulier de quasigroupe (S,*) qui possède un élément neutre. Autrement dit, il existe un élément qui ne modifie pas les autres lors de l'opération : $$ a * e = a $$ et $$ e * a = a $$ pour tout élément \(a\) de S.
Comme dans tout quasigroupe, la structure (S,*) exige que, pour chaque paire d'éléments \(a\) et \(b\), il existe des éléments uniques appelés inverses à gauche et inverses à droite, tels que :
$$ a * d_x = b $$ $$ s_x * a = b $$
La grande différence entre une boucle et un quasigroupe « ordinaire » réside donc dans la présence de cet élément neutre, qui joue un rôle central dans la structure.
Dans une boucle, pour chaque paire \(a, b\), il existe un unique élément \(x\) appartenant à S qui satisfait simultanément :
$$ a * x = b $$ $$ x * a = b $$
Les boucles font partie de la vaste famille des structures groupoïdes, des systèmes algébriques où l'on étudie la cohérence des opérations plutôt que leur nature numérique.
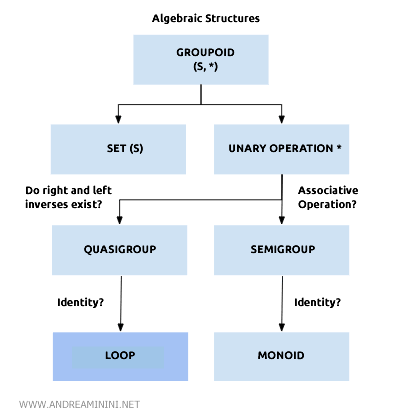
Et si, en plus, l'opération * est associative, la boucle devient une boucle associative - autrement dit, un groupe.
Un exemple concret
Prenons l'ensemble des nombres rationnels non nuls, noté Q - {0}, muni de la multiplication (·). Cet ensemble forme une boucle : $$ (Q - \{ 0 \}, \cdot) $$
Pourquoi ? Parce que la multiplication est une opération fermée : le produit de deux nombres rationnels non nuls reste toujours dans Q - {0}.
$$ \forall a, b \in Q - \{ 0 \} \Longrightarrow a \cdot b \in Q - \{ 0 \} $$
Cette propriété garantit que (Q - {0},·) répond aux critères d'un groupoïde.
Exemple : Si a = 4 et b = 7, leur produit est encore un nombre rationnel: $$ a \cdot b = 4 \cdot 7 = 28 $$
De plus, pour toute paire d'éléments \(a\) et \(b\), il existe un élément unique qui agit comme inverse à gauche et à droite.
La structure (Z,·) est donc un quasigroupe.
Exemple détaillé : Si a = 4 et b = 7, l'inverse \(x\) est \(7/4\) : $$ a \cdot x = b $$ $$ 4 \cdot x = 7 $$ $$ x = \frac{7}{4} $$ Et le même élément \(y = 7/4\) vérifie aussi : $$ y \cdot a = b $$ $$ y \cdot 4 = 7 $$ $$ y = \frac{7}{4} $$ On voit donc que les inverses à gauche et à droite coïncident.
Dans la structure (Q - {0},·), l'élément neutre est le nombre \(e = 1\) :
$$ \forall a \in Q - \{ 0 \} \Longrightarrow a \cdot 1 = 1 \cdot a = a $$
On peut donc affirmer que (Q - {0},·) est bien une boucle.
Remarque : La multiplication étant associative, (Q - {0},·) est non seulement une boucle, mais aussi une boucle associative - c'est-à-dire un groupe. En résumé : tout groupe est une boucle, mais toutes les boucles ne sont pas des groupes.
Les boucles occupent une position fascinante dans la hiérarchie des structures algébriques : elles prolongent la logique des quasigroupes tout en préparant le terrain pour la rigueur des groupes. Ce sont des outils puissants pour comprendre comment les mathématiques décrivent la symétrie, la composition et l'équilibre des opérations.