Les quasigroupes
Un quasigroupe est un groupoïde (S,*) dans lequel, pour chaque paire d’éléments a et b, on peut toujours trouver un inverse à droite (dx) et un inverse à gauche (sx) qui permettent de résoudre les équations suivantes : $$ a * d_x = b $$ et $$ s_x * a = b $$
Autrement dit, dans un quasigroupe, toute équation du type a * x = b ou y * a = b possède une solution unique. C’est ce qui distingue cette structure au sein de la grande famille des groupoïdes.
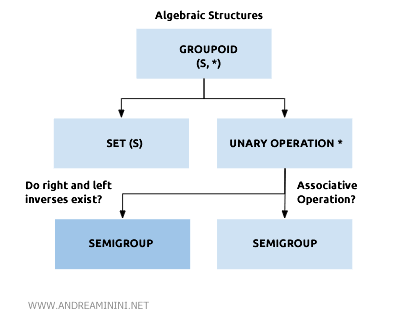
Les quasigroupes ne sont pas forcément commutatifs : l’ordre des opérations a de l’importance. Mais s’ils possèdent en plus un élément neutre (un élément qui ne modifie pas les autres lors de l’opération), on les appelle des loops - ou boucles en français.
Un exemple simple
Pour rendre cette idée plus concrète, prenons l’ensemble des nombres entiers Z avec l’opération de soustraction (-). Cette structure est un quasigroupe : $$ (Z,-) $$
Pourquoi ? Parce que la soustraction est une opération fermée sur les entiers : la différence de deux entiers reste toujours un entier.
$$ \forall a, b \in Z \Longrightarrow a - b \in Z $$
La structure (Z,-) est donc un groupoïde.
Exemple : Prenons a = 4 et b = 7. On a : $$ a - b = 4 - 7 = -3 $$ Le résultat est bien un entier.
De plus, pour tout couple d’entiers (a, b), on peut déterminer un inverse à droite et un inverse à gauche qui permettent de retrouver b à partir de a.
C’est ce qui fait de (Z,-) un véritable quasigroupe.
Exemple détaillé :
Si a = 4 et b = 7 :
L’inverse à droite x = -3 vérifie :
$$ a - x = b $$
$$ 4 - x = 7 $$
$$ x = 4 - 7 $$
$$ x = -3 $$
Tandis que l’inverse à gauche y = 11 satisfait :
$$ y - a = b $$
$$ y - 4 = 7 $$
$$ y = 7 + 4 $$
$$ y = 11 $$
En résumé, les quasigroupes sont des structures algébriques fascinantes : ils généralisent l’idée de groupe en relâchant certaines contraintes, tout en conservant une remarquable cohérence interne. Ils sont largement utilisés en mathématiques abstraites, en cryptographie et même en conception de systèmes algébriques appliqués.