Matrices inversibles et matrices inverses

En algèbre linéaire, une matrice carrée $ A $ d’ordre $ n $ est dite inversible s’il existe une autre matrice carrée de même ordre, appelée matrice inverse et notée $ A^{-1} $, telle que $ A \cdot A^{-1} = I $ et $ A^{-1} \cdot A = I $, où $ I $ désigne la matrice identité.

matrice inversible

En notation matricielle, l’inverse est indiqué par l’exposant −1, à l’image de la notation de l’inverse multiplicatif en arithmétique.

Remarque. L’idée de matrice inverse est analogue à celle du réciproque d’un nombre réel : tout nombre réel non nul possède un inverse multiplicatif $ \tfrac{1}{a} $ vérifiant $ a \cdot \tfrac{1}{a} = 1 $. De même, si une matrice $ M $ est inversible, il existe $ M^{-1} $ tel que $ M \cdot M^{-1} = I $, où $ I $ joue le rôle de neutre multiplicatif : $ M \cdot I = M $.

Toutes les matrices ne sont pas inversibles : en réalité, nombre d’entre elles n’admettent pas d’inverse.

L’ensemble de toutes les matrices inversibles d’ordre $ n $ à coefficients réels se note $ \text{GL}_n(\mathbb{R}) $ ou $ \text{GL}(n,\mathbb{R}) $.

$$ \text{GL}(n, \mathbb{R}) $$

Cet ensemble est appelé le groupe linéaire général d’ordre $ n $ sur le corps des réels.

Remarque. L’ensemble $ \text{GL}_n(\mathbb{R}) $ est stable par multiplication : le produit de deux matrices inversibles du même ordre est encore une matrice inversible. De plus, la matrice identité $ I $ appartient à $ \text{GL}_n(\mathbb{R}) $.

Exemple de matrice inverse
Calcul de la matrice inverse : deux approches
Propriétés des matrices inverses

Exemple de matrice inverse

Considérons la matrice suivante :

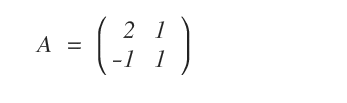
une matrice

Cette matrice est inversible, c’est-à-dire qu’il existe une matrice $ A^{-1} $ telle que $ A \cdot A^{-1} = I_{(2)} $, où $ I_{(2)} $ désigne la matrice identité d’ordre 2.

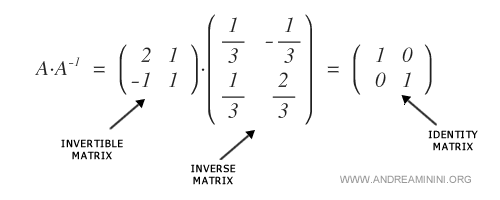
exemple

Calcul de la matrice inverse : deux approches

On distingue principalement deux méthodes pour calculer l’inverse d’une matrice inversible :

Remarque. La seconde méthode est en général plus efficace sur le plan algorithmique, tandis que la première met en évidence les aspects conceptuels du lien entre matrices et systèmes linéaires.

Méthode 1

Soit une matrice $ A $. On cherche à savoir si elle est inversible et, le cas échéant, à déterminer son inverse $ A^{-1} $.

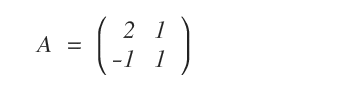
Exemple de matrice :

Si $ A $ est inversible, on doit avoir $ A \cdot A^{-1} = I $.

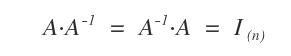
Matrice inversible :

Pour le vérifier, on suppose que $ A $ est multipliée par une matrice $ B $ à coefficients inconnus, et l’on impose que le produit soit égal à la matrice identité.

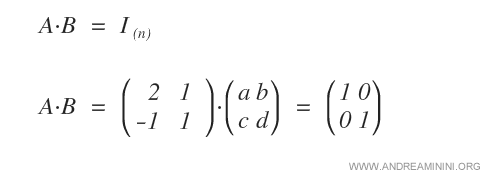
Produit de A par une matrice d’inconnues égal à l’identité

Le développement du produit ligne par colonne conduit à un système d’équations linéaires.

Système d’équations linéaires équivalent

La résolution de ce système permet de déterminer les coefficients de $ A^{-1} $. Si le système est compatible et déterminé, la matrice $ A $ est bien inversible.

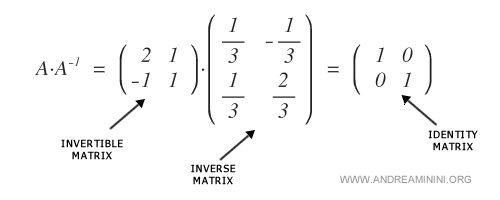
Calcul de la matrice inverse :

Remarque. Bien que ce procédé soit instructif et utile à des fins pédagogiques, il devient vite impraticable pour des matrices de grande dimension. Dans ce cas, la seconde méthode est à privilégier.

Méthode 2

Pour une matrice $ 1 \times 1 $, son inverse est simplement $ A^{-1} = a_{11}^{-1} $. Pour les matrices d’ordre supérieur, on applique la formule : $$ A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A) $$ où $ \text{adj}(A) $ désigne la matrice adjointe.

Le théorème d’existence stipule qu’une matrice est inversible si, et seulement si, son déterminant est non nul.

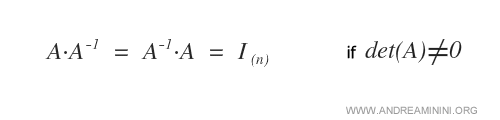
Théorème d’existence de la matrice inverse :

Lorsque $ \det(A) \neq 0 $, la matrice est inversible. Pour calculer son inverse, on procède en trois étapes : 1) on construit la matrice des cofacteurs, 2) on la transpose pour obtenir l’adjointe, 3) on multiplie le tout par le scalaire $ \tfrac{1}{\det(A)} $.

Remarque. Si $ \det(A) = 0 $, la matrice n’est pas inversible et le processus s’arrête là.

Propriétés des matrices inverses

Seules les matrices carrées peuvent être inversibles. Si une matrice est inversible, son inverse est nécessairement unique.
L’inverse d’une matrice ne s’obtient pas en inversant individuellement chacun de ses coefficients. Ses entrées peuvent différer radicalement de celles de $ A $, même si, dans certains cas particuliers, elles coïncident. Par exemple, l’inverse de la matrice identité est elle-même.
Si $ A $ est inversible, alors $ A^{-1} $ l’est également, et l’on a : $ (A^{-1})^{-1} = A $.
Le déterminant de $ A^{-1} $ est l’inverse de celui de $ A $ : $$ \det(A^{-1}) = \frac{1}{\det(A)} $$
La transposée d’une matrice inversible est elle aussi inversible : $$ (A^{T})^{-1} = (A^{-1})^{T} $$
Si $ A $ et $ B $ sont inversibles, alors leur produit l’est également, et l’on a : $$ (AB)^{-1} = B^{-1}A^{-1} $$
Une matrice de déterminant nul n’est pas inversible. Seules les matrices non singulières (celles dont le déterminant est non nul) possèdent une inverse.
L’existence de l’inverse entraîne son unicité.