Calcul de l’inverse d’une matrice par élimination de Gauss
L’élimination de Gauss est une méthode alternative permettant de déterminer l’inverse d’une matrice.
Elle est particulièrement utile pour les matrices de grande dimension, lorsque les formules directes deviennent trop lourdes à manipuler.
Procédure pas à pas : inversion d’une matrice avec l’élimination de Gauss
On commence par placer la matrice identité I à droite de la matrice M.
On obtient ainsi la matrice augmentée, notée M|I.
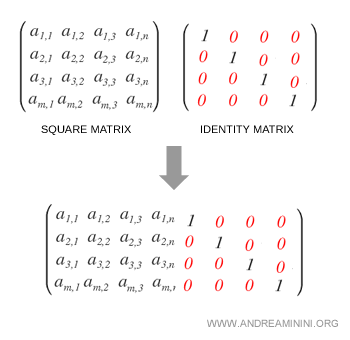
Dans cette matrice augmentée, l’identité figure dans le bloc de droite (indiqué en rouge).
L’objectif est d’appliquer des opérations élémentaires sur les lignes jusqu’à transformer le bloc de gauche en matrice identité.

Remarque. Les opérations élémentaires sur les lignes consistent à : échanger deux lignes, multiplier une ligne par un scalaire non nul k, ou ajouter à une ligne un multiple d’une autre.
Une fois le bloc de gauche réduit à l’identité, le bloc de droite représente alors la matrice inverse de M.

Un exemple détaillé
Considérons la matrice 2×2 :
$$ M = \begin{pmatrix} 2 & 1 \\ -1 & 1 \end{pmatrix} $$
Nous voulons calculer son inverse, M-1, en utilisant l’élimination de Gauss.
On ajoute la matrice identité 2×2 à droite :
$$ M|I = \begin{pmatrix} 2 & 1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{pmatrix} $$
Nous allons ensuite transformer le bloc de gauche en identité en appliquant des opérations élémentaires.
Première étape : échanger les deux lignes : R1 ⇔ R2
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 & 1 & 1 & 0 \end{pmatrix} $$
Deuxième étape : ajouter deux fois la première ligne à la seconde : R2 = R2 + 2·R1
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 + (-1) \cdot 2 & 1 + 1 \cdot 2 & 1 + 0 \cdot 2 & 0 + 1 \cdot 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ \color{red}0 & 3 & 1 & 2 \end{pmatrix} $$
On élimine maintenant l’élément situé au-dessus du 3 en retranchant un tiers de la deuxième ligne à la première : R1 = R1 + (−1/3)·R2
$$ M|I = \begin{pmatrix} -1 - 0 \cdot \frac{1}{3} & 1 - 3 \cdot \frac{1}{3} & 0 - 1 \cdot \frac{1}{3} & 1 - 2 \cdot \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} -1 & \color{red}0 & - \frac{1}{3} & \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
On multiplie ensuite la première ligne par −1 : R1 = (−1)·R1
$$ M|I = \begin{pmatrix} -1 \cdot (-1) & 0 \cdot (-1) & - \frac{1}{3} \cdot (-1) & \frac{1}{3} \cdot (-1) \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} \color{red}1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
Enfin, on divise la deuxième ligne par 3 : R2 = (1/3)·R2
$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 \cdot \frac{1}{3} & 3 \cdot \frac{1}{3} & 1 \cdot \frac{1}{3} & 2 \cdot \frac{1}{3} \end{pmatrix} $$
$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
À ce stade, le bloc de gauche est exactement la matrice identité.
$$ M|I = \begin{pmatrix} \color{red} 1 & \color{red}0 & \frac{1}{3} & - \frac{1}{3} \\ \color{red}0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
On en conclut que M est bien inversible.
La matrice inverse correspond alors au bloc de droite :
$$ M^{-1} = \begin{pmatrix} \frac{1}{3} & - \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
Remarque. J’ai également résolu cet « exemple » en utilisant d’autres méthodes de calcul d’inverses, et, naturellement, le résultat obtenu est identique.