Groupe linéaire général
Le groupe linéaire général
En algèbre linéaire, le groupe linéaire général (GL) est l’ensemble de toutes les matrices inversibles d’ordre n définies sur un corps K. On l’appelle aussi groupe matriciel, et on le note GL(n,K) ou GLn(K).
La notion de groupe linéaire général a été introduite pour la première fois en 1832 par Évariste Galois.
Une matrice est dite inversible lorsqu’elle est non singulière, c’est-à-dire quand son déterminant est différent de zéro.
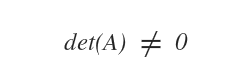
De cette façon, le groupe linéaire général (GL) des matrices réelles inversibles d’ordre n se définit ainsi :
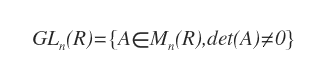
Explication. Toute matrice A de taille n×n dont le déterminant est non nul appartient au groupe linéaire général GL.
Exemple
Voici un exemple de matrice appartenant au groupe linéaire général d’ordre 2 :
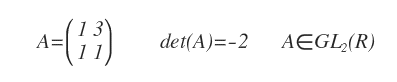
Groupe linéaire spécial
Le groupe linéaire spécial (SL) est constitué des matrices carrées réelles d’ordre n dont le déterminant vaut exactement 1. Il s’agit d’un sous-groupe de GL.
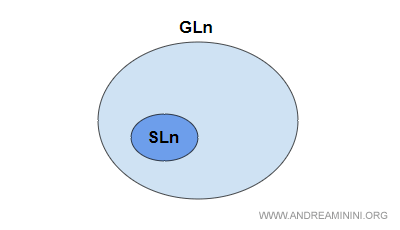
On le note SL(n,K) ou, de façon équivalente, SLn(K).
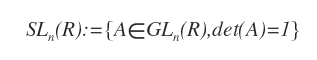
Explication. Toute matrice A appartenant à GLn et de déterminant égal à 1 fait aussi partie du groupe linéaire spécial SLn.
Exemple
La matrice suivante est un exemple d’élément du groupe linéaire spécial d’ordre 2 :
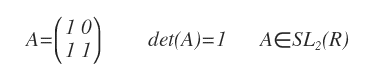
Le groupe orthogonal spécial
Le groupe orthogonal spécial est un sous-groupe du groupe linéaire spécial SLn. Il est formé par les matrices orthogonales réelles d’ordre n dont le déterminant est égal à 1.
On le note SOn.
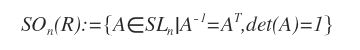
Autrement dit, le groupe orthogonal spécial peut être vu comme l’intersection entre le groupe linéaire spécial SLn et l’ensemble On des matrices orthogonales d’ordre n.
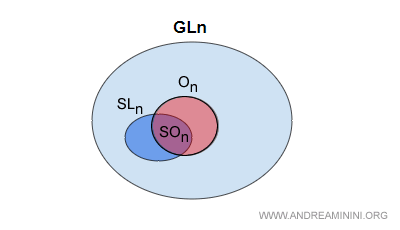
Différence entre le groupe orthogonal spécial et le groupe orthogonal général. Le groupe orthogonal spécial SOn est un sous-groupe de SLn. À l’inverse, le groupe orthogonal général On regroupe toutes les matrices orthogonales de déterminant +1 ou −1. Ce dernier est lui-même un sous-groupe du groupe linéaire général GLn.
Exemple
La matrice suivante est un élément du groupe orthogonal spécial SO2 d’ordre 2 :
