Singularité d’une matrice
En algèbre linéaire, la singularité d’une matrice est une propriété directement liée au déterminant d’une matrice carrée.
Qu’est-ce qu’une matrice singulière ?
On appelle matrice singulière une matrice carrée A dont le déterminant, noté det(A), est nul. Autrement dit, une matrice est singulière dès que son déterminant s’annule.
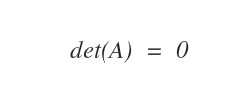
Matrice non singulière
À l’inverse, une matrice carrée A est dite non singulière lorsque son déterminant, det(A), est différent de zéro.
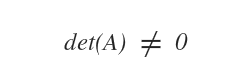
Pourquoi la singularité est-elle importante ?
La singularité d’une matrice indique si cette matrice est inversible ou non. C’est donc un critère fondamental en algèbre linéaire.
Une matrice carrée est inversible si, et seulement si, elle n’est pas singulière.