Diagonale principale d'une matrice carrée

La diagonale principale d'une matrice carrée d'ordre n est formée des éléments dont l'indice de ligne est identique à l'indice de colonne. En d'autres termes : $$ a_{11}, \ a_{22}, \ a_{33}, \ ... , \ a_{nn} . $$

Elle s'étend du coin supérieur gauche jusqu'au coin inférieur droit de la matrice.

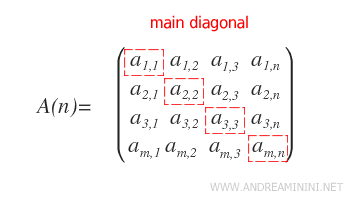
Remarque : la diagonale principale n'existe que dans les matrices carrées, c'est-à-dire celles qui possèdent le même nombre de lignes et de colonnes.

Exemple

Considérons une matrice carrée d'ordre n = 3, c'est-à-dire composée de trois lignes et de trois colonnes.

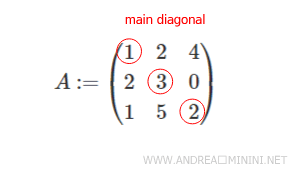
Dans cette illustration, la diagonale principale d'une matrice 3×3 est mise en évidence.

Les éléments qui la composent sont les suivants :

$$ a_{11} = 1 $$

$$ a_{22} = 3 $$

$$ a_{33} = 2 $$

et ainsi de suite, selon la dimension de la matrice.