Matrice symétrique
Qu’est-ce qu’une matrice symétrique ?
Une matrice symétrique est une matrice carrée d’ordre \( n \) dont les éléments sont disposés de manière réfléchie par rapport à la diagonale principale.
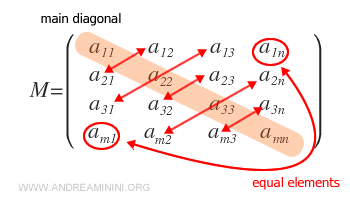
Formellement, on a la relation \( a_{ij} = a_{ji} \) pour tout couple d’indices \( i, j = 1, ..., n \).
![]()
Remarque : seules les matrices carrées peuvent être symétriques. Les matrices rectangulaires ( \( m \neq n \) ) ne le peuvent pas, car leur structure ne correspond pas à celle de leur transposée. De plus, seules les matrices carrées possèdent une diagonale principale bien définie.
Par convention, on note les matrices symétriques \( M^S \), où « S » signifie « symétrique ».
L’ensemble de toutes les matrices symétriques se note \( S(n, R) \), où \( n \) est l’ordre de la matrice et \( R \) l’ensemble des réels.
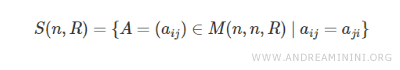
Cet ensemble \( S(n, R) \) est un sous-ensemble de l’espace des matrices carrées à coefficients réels, noté \( M(n, n, R) \).
Un exemple concret
La matrice suivante possède trois lignes ( \( m = 3 \) ) et trois colonnes ( \( n = 3 \) ) : elle est donc carrée ( \( m = n \) ).
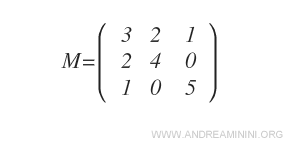
Étant carrée, elle possède une diagonale principale bien définie.
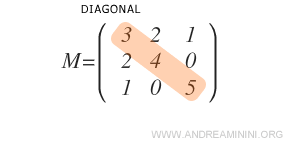
Pour vérifier la symétrie, on compare les éléments situés au-dessus et au-dessous de cette diagonale.
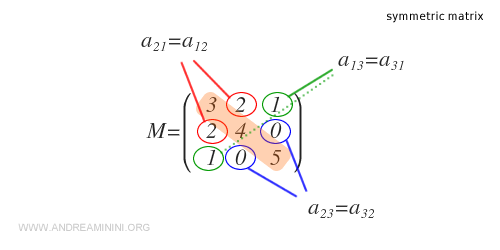
Dans ce cas, la matrice est symétrique car, en échangeant lignes et colonnes, les valeurs de ses éléments restent inchangées.
Remarque : une matrice carrée qui ne satisfait pas la condition de symétrie n’est pas considérée comme symétrique.
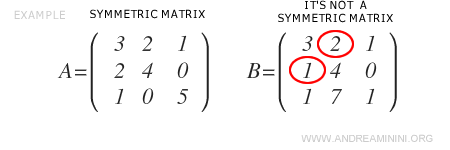
La transposée d’une matrice symétrique
Une matrice symétrique \( M \) coïncide toujours avec sa transposée \( M^T \).
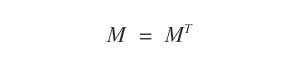
Exemple : la matrice \( M \) ci-dessous est symétrique ; elle est donc identique à sa transposée \( M^T \). En échangeant lignes et colonnes, chaque élément \( a_{ij} \) demeure inchangé.
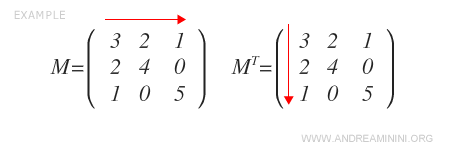
Comment construire une matrice symétrique
Toute matrice carrée d’ordre \( n \) peut être transformée en matrice symétrique.
On obtient sa version symétrique à l’aide de la formule suivante :
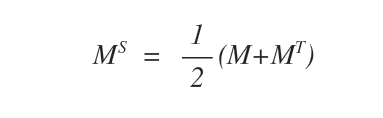
Un autre exemple pratique
Considérons la matrice carrée d’ordre 3 ci-dessous, qui n’est pas symétrique.
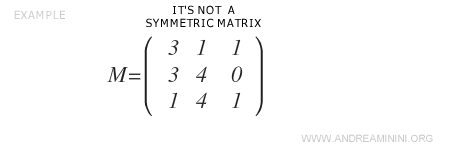
Pour la rendre symétrique, on calcule d’abord sa transposée \( M^T \).
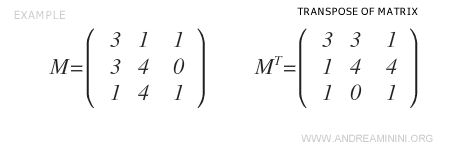
On applique ensuite la formule \( \tfrac{1}{2} \cdot (M + M^T) \).
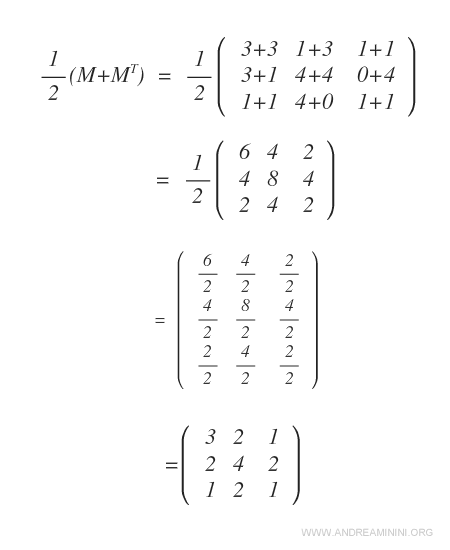
On obtient ainsi la matrice symétrique \( M_s \), dont les éléments sont disposés symétriquement par rapport à la diagonale principale.
Différences entre matrices symétriques et antisymétriques
Dans une matrice symétrique, on a \( a_{ij} = a_{ji} \).
Dans une matrice antisymétrique, en revanche, \( a_{ij} = -a_{ji} \).
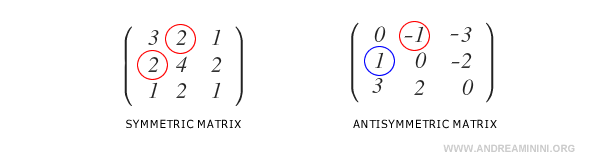
Remarque : le fait qu’une matrice ne soit pas symétrique n’implique pas qu’elle soit antisymétrique. Les ensembles des matrices symétriques \( S_n(R) \) et antisymétriques \( A_n(R) \) sont deux sous-ensembles distincts de l’espace \( M_n(R) \). Ils n’ont qu’un seul élément en commun : la matrice nulle, qui est à la fois symétrique et antisymétrique.
Résumé : propriétés essentielles des matrices symétriques
Parmi les propriétés fondamentales des matrices symétriques, on peut retenir :
- Toute matrice nulle est symétrique.
- La somme d’une matrice symétrique \( M^S \) et d’une matrice antisymétrique \( M^{AS} \) reconstitue la matrice d’origine \( M \).
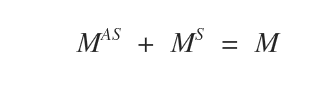
- Toute matrice diagonale \( D(n, R) \) est nécessairement une matrice symétrique \( S(n, R) \).
Démonstration : les matrices diagonales \( D(n, R) \) sont carrées et partagent les caractéristiques structurelles des matrices symétriques \( S(n, R) \) :
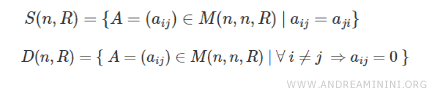
Dans une matrice diagonale \( D(n, R) \), deux cas se présentent :
1) Si \( i \neq j \), alors \( a_{ij} = 0 \), et donc \( a_{ji} = 0 \), ce qui respecte la condition de symétrie.
2) Si \( i = j \), alors \( a_{ij} = a_{ji} \), puisqu’il s’agit du même élément.
Par conséquent, toute matrice diagonale est symétrique.