Théorème de la matrice augmentée

Le théorème de la matrice augmentée constitue une méthode particulièrement efficace pour déterminer le rang d’une matrice, sans avoir à calculer l’ensemble des mineurs d’ordre k.

On le désigne également sous les appellations méthode d’augmentation, théorème d’Orlando ou encore théorème de Kronecker.

Définition

Soit b un mineur non nul d’ordre k, correspondant à une sous-matrice B de la matrice A.

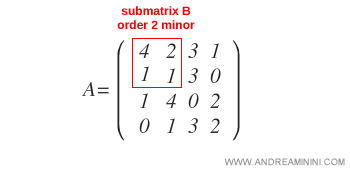
Remarque. Le mineur correspond au déterminant de la sous-matrice B : $$ \Delta_B = 4 \cdot 1 - 2 \cdot 1 = 2 $$

Si tous les mineurs d’ordre k+1 obtenus en augmentant la sous-matrice B s’annulent...

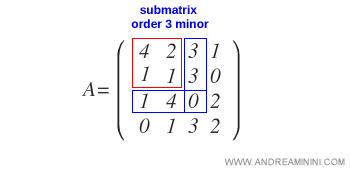
Que signifie augmenter une sous-matrice ? C’est comparable à l’ajout d’une bordure à une couverture : on adjoint à la sous-matrice initiale d’ordre k une ligne et une colonne supplémentaires, choisies parmi celles de la matrice qui n’ont pas encore été utilisées. On obtient ainsi une sous-matrice d’ordre k+1. Les mineurs correspondants sont appelés augmentations de B.

Si tous les mineurs d’ordre k+1 sont nuls, le rang de la matrice A est exactement k.

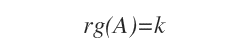
Remarque. Une même sous-matrice B peut être augmentée de plusieurs façons. Selon la manière dont on combine les lignes et colonnes restantes de A, on obtient différentes sous-matrices augmentées. Dans ce cas, il existe 4 combinaisons possibles, et donc quatre sous-matrices dont les mineurs doivent être évalués.

 

Exemple concret

Considérons la matrice 4x4 suivante, dont le rang peut varier entre 0 et 4.

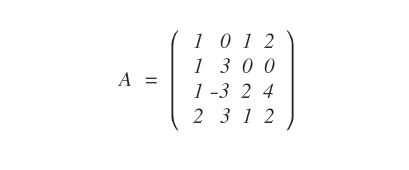
Comme elle contient au moins un élément non nul, son rang est nécessairement compris entre 1 et 4.

Pour vérifier si le rang est au moins égal à 2, calculons le déterminant d’une sous-matrice d’ordre 2� - 2.

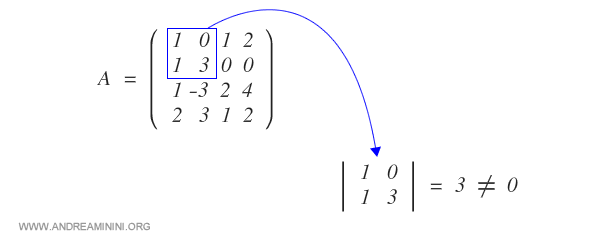
Étant donné que ce mineur d’ordre 2 est non nul, le rang se situe entre 2 et 4.

Nous appliquons alors le théorème de la matrice augmentée à cette sous-matrice afin de déterminer si le rang peut atteindre 3.

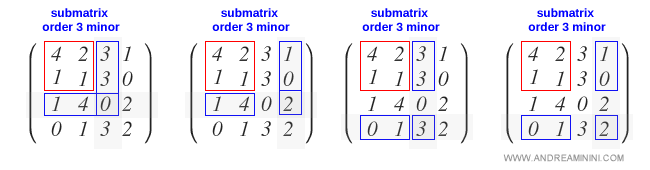
Cette sous-matrice peut être augmentée de quatre manières différentes :

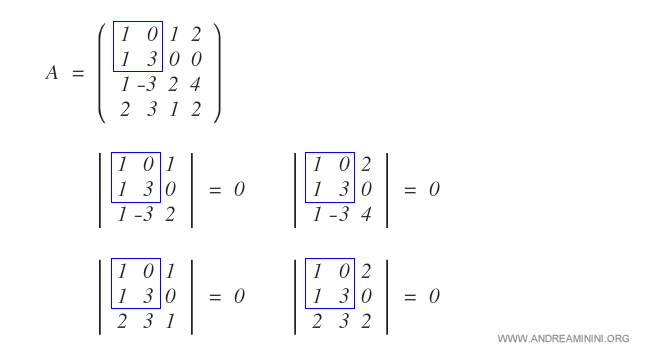
Dans chacun de ces cas, les mineurs des sous-matrices augmentées s’avèrent nuls.

Selon le théorème de la matrice augmentée, la matrice A ne peut donc pas avoir un rang égal à 3.

Et si son rang n’est pas 3, il ne peut évidemment pas être supérieur (k > 3).

On conclut ainsi que le rang maximal de cette matrice est k = 2, autrement dit : $$ rk(A) = 2 $$

Observations utiles

Voici quelques observations essentielles relatives au théorème de la matrice augmentée :

• Une matrice a un rang $$ rk(M) = 0 $$ si et seulement si c’est la matrice nulle.

  Démonstration. Si M est la matrice nulle (tous ses éléments sont nuls), alors tous ses mineurs d’ordre 1 le sont également.

• Le rang d’une matrice M est identique à celui de sa transposée M^T : $$ rk(M) = rk(M^T) $$

  Explication. Une matrice carrée et sa transposée ont le même déterminant. Le rang est donc conservé par transposition.

• Si une matrice M a un rang $$ rk(M) = n $$, alors tous ses mineurs d’ordre supérieur à n sont nécessairement nuls.
• Si tous les mineurs d’ordre n sont nuls, alors le rang de la matrice est strictement inférieur à n : $$ rk(M) < n $$

Et l’on peut poursuivre le raisonnement de manière analogue pour des ordres supérieurs.