Détermination du rang par l’élimination de Gauss

Le rang d’une matrice peut être déterminé de façon particulièrement efficace grâce à la procédure d’élimination de Gauss.

Soit A une matrice de dimension m × n et soit B une forme échelonnée par lignes obtenue à partir de A au moyen de l’élimination de Gauss. Le rang de A est alors exactement égal au nombre de positions pivots figurant dans B.

Exemple concret

Calculons le rang de la matrice A suivante.

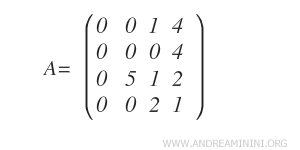
En appliquant l’élimination de Gauss, nous transformons la matrice A en une matrice échelonnée par lignes, que nous notons B.

La matrice B est équivalente par lignes à la matrice initiale A.

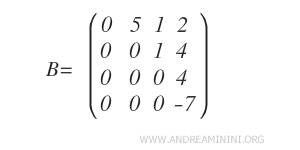
On constate ici que la matrice B présente trois positions pivots.

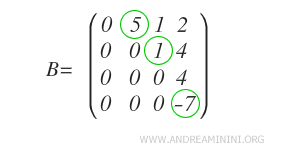
Remarque. On appelle pivot le premier élément non nul d’une ligne (lu de gauche à droite), situé au-dessus de zéros dans sa colonne. Dans ce contexte, il n’est pas requis que le pivot soit normalisé à 1.

On en déduit que le rang de la matrice A est égal à 3.

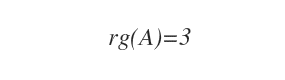
Cette méthode permet donc de déterminer le rang d’une matrice sans recourir au calcul exhaustif des mineurs.

Il s’agit d’une technique à la fois efficace et universellement employée en algèbre linéaire pour établir le rang d’une matrice.