Calcul de l’inverse d’une matrice par la méthode de Gauss-Jordan
Dans cette section, nous appliquons la méthode de Gauss-Jordan afin de déterminer l’inverse A-1 d’une matrice carrée A supposée inversible.
Qu’est-ce que la méthode de Gauss-Jordan ? Il s’agit d’un procédé systématique permettant de réduire une matrice soit en forme échelonnée par lignes, soit en forme échelonnée réduite.
Principe du calcul de l’inverse
On commence par construire la matrice augmentée [A | I], obtenue en accolant à A la matrice identité de même ordre.
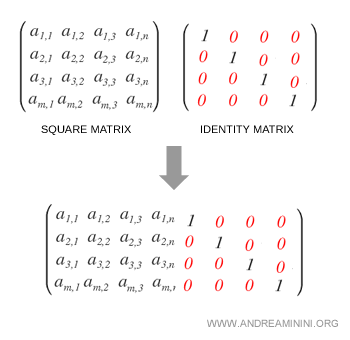
L’algorithme consiste ensuite à transformer cette matrice augmentée en [I | A-1].
Remarque : Les opérations autorisées sont l’échange de deux lignes, la multiplication d’une ligne par un scalaire non nul et l’addition à une ligne d’un multiple d’une autre. Enchaînées de façon appropriée, elles permettent d’annuler tous les coefficients non pivots.

Lorsque le bloc de gauche est réduit à l’identité, le bloc de droite fournit directement l’inverse de A.

La méthode précise rigoureusement la suite des opérations à effectuer, ce qui en fait un outil idéal pour les calculs systématiques et la mise en œuvre algorithmique.
Différence avec l’élimination de Gauss : Dans les deux cas, il s’agit de transformer [A | I] en [I | A-1]. L’élimination de Gauss autorise une certaine liberté dans l’ordre des opérations, ce qui est pratique pour les calculs à la main. La méthode de Gauss-Jordan impose au contraire une séquence stricte d’étapes, particulièrement adaptée aux traitements automatiques.
Exemple détaillé
Considérons la matrice carrée A et cherchons son inverse A-1 :
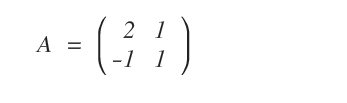
On construit la matrice augmentée en accolant l’identité I d’ordre 2 :
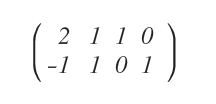
L’objectif est de transformer le bloc gauche en identité par une suite d’opérations de lignes.
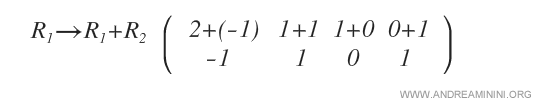
On obtient un premier pivot, égal à 1, sur la diagonale principale.

On annule l’élément situé sous ce pivot (−1) en appliquant la formule de Gauss-Jordan.
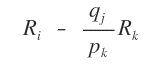
Ici, \( q_j \) désigne l’entrée à annuler (−1), \( p_k \) le pivot (1), et \( R_i, R_k \) les lignes concernées. Le rapport est \( q_j/p_k = -1 \).
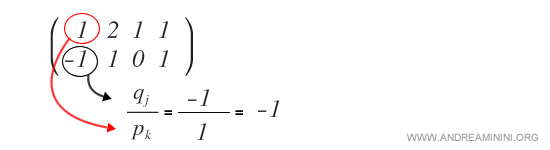
On applique alors l’opération \( R_2 - (q_j/p_k)\cdot R_1 \) à toute la deuxième ligne.
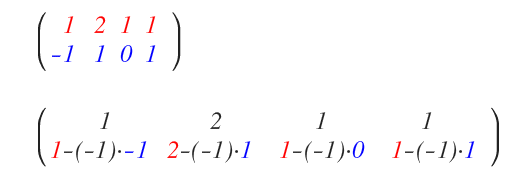
La colonne sous le pivot est ainsi annulée ; la première colonne est réduite.

On passe à la deuxième colonne. Le pivot vaut 3 ; on le normalise en multipliant la deuxième ligne par 1/3 :
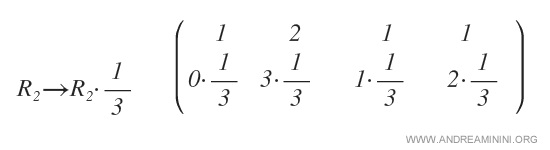
On obtient ainsi un second pivot, égal à 1, sur la diagonale.

Il reste un élément non nul au-dessus de ce pivot (2, dans la première ligne). On l’élimine par l’opération \( R_1 - (q_j/p_k)\cdot R_2 \), avec \( q_j = 2 \) et \( p_k = 1 \), soit un rapport de 2.
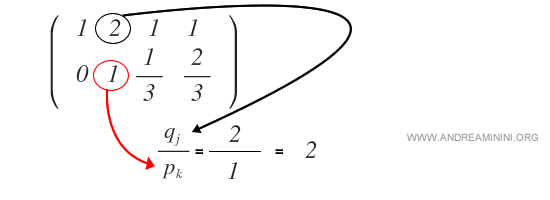
On met à jour la première ligne :
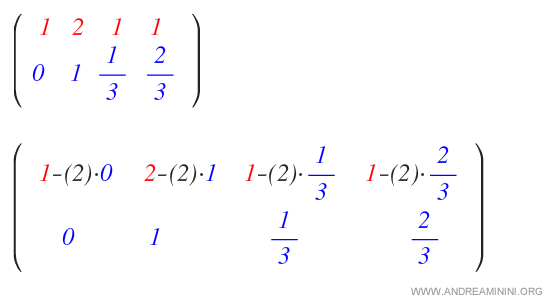
Le 2 de la seconde colonne est ainsi supprimé.
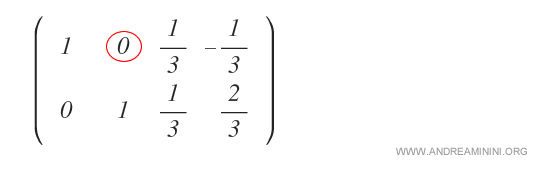
Le bloc de gauche est désormais l’identité.
Par conséquent, la matrice A est inversible, et le bloc de droite fournit son inverse A-1 :
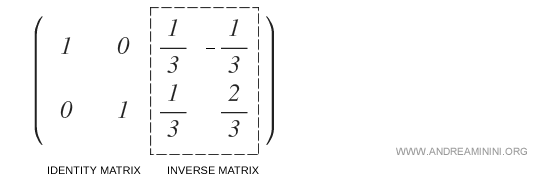
La matrice inverse de A est donc :
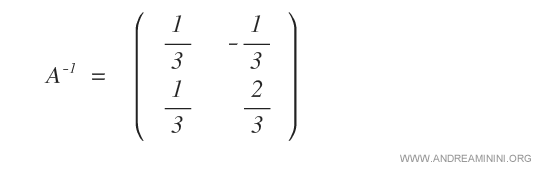
Pour vérification, on calcule le produit A · A-1, qui redonne bien l’identité I :
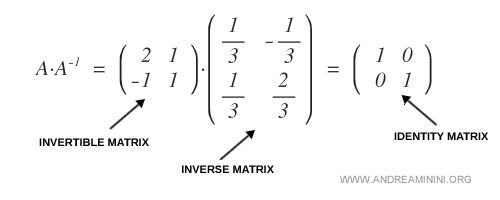
Remarque : Le même résultat est obtenu en utilisant d’autres méthodes de calcul de l’inverse, ce qui confirme la validité du procédé de Gauss-Jordan.