Méthode d’élimination de Gauss

La méthode d’élimination de Gauss est une technique systématique qui permet de déterminer l’ensemble des solutions possibles d’un système d’équations linéaires.

Remarque : Par convention, on applique l’élimination de Gauss sur les lignes de la matrice. Toutefois, il est tout à fait possible de l’utiliser aussi sur les colonnes, et dans certaines situations pratiques cette approche peut être plus commode.

On parle parfois de méthode de Gauss-Jordan, qui n’est en réalité qu’une variante de la méthode de Gauss.

Quel est l’objectif ?

Cette méthode vise à transformer un système d’équations linéaires en un système échelonné.

Une fois le système sous cette forme, il devient beaucoup plus simple de calculer le rang et de résoudre les équations, en particulier lorsque le nombre d’inconnues et d’équations est élevé.

Principe de la méthode de Gauss

Le but est de réduire la matrice initiale à une matrice équivalente plus facile à étudier.

Qu’appelle-t-on matrice équivalente ? C’est une matrice dont les systèmes linéaires associés sont équivalents. Ainsi, le système lié à la matrice équivalente M' admet exactement les mêmes solutions que celui de la matrice initiale M, mais son analyse est bien plus simple.

Le procédé de Gauss-Jordan consiste à transformer la matrice de départ en une matrice échelonnée (ou forme échelonnée).

Chaque premier élément non nul d’une ligne, situé le plus à gauche, est appelé pivot.

Remarque : Le pivot est le premier coefficient non nul d’une ligne non nulle. On le désigne aussi sous le nom de terme directeur.

Propriétés d’une matrice échelonnée

Une matrice échelonnée présente les caractéristiques suivantes :

1. Toutes les lignes nulles sont regroupées en bas.
   
   

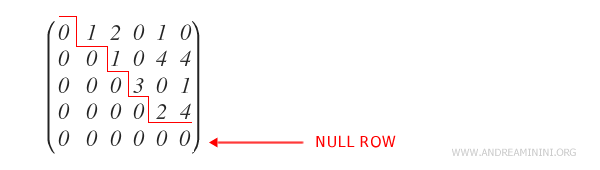
   Qu’est-ce qu’une ligne nulle ? C’est une ligne dont tous les éléments sont égaux à zéro.

2. Dans chaque ligne non nulle, le pivot apparaît dans une colonne plus à droite que le pivot de la ligne précédente.
   

Pour obtenir la forme échelonnée d’une matrice équivalente, on utilise un ensemble d’opérations élémentaires appelées opérations de Gauss.

Quelles sont les opérations de Gauss ?

Les transformations élémentaires admises sur une matrice, d’après Gauss, sont les suivantes :

1. Permuter deux lignes.
   
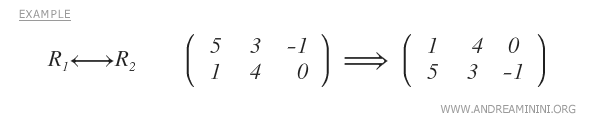
2. Multiplier une ligne par un nombre réel non nul.
   
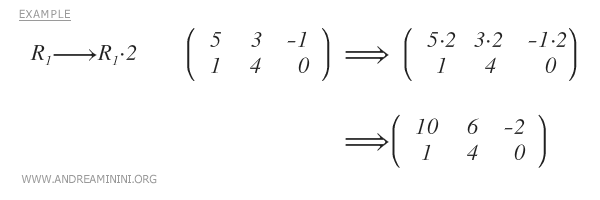
3. Ajouter à une ligne un multiple d’une autre ligne.
   

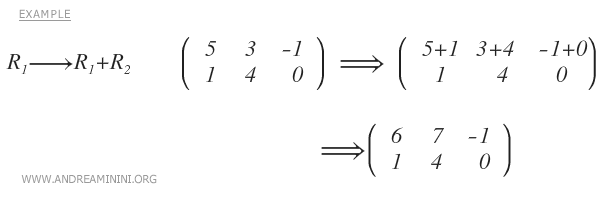
Remarque : Les deux dernières opérations peuvent se combiner en une seule : ajouter à une ligne un multiple d’une autre.

Algorithme de Gauss

Soit une matrice A de m lignes et n colonnes. L’objectif est de la transformer en une matrice équivalente sous forme échelonnée.

Remarque : Si la matrice est entièrement nulle, l’algorithme s’arrête immédiatement.

Étape 1

Repérer la première colonne j non nulle de A, en parcourant de gauche à droite.

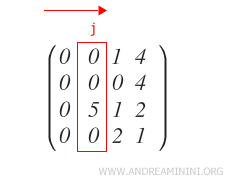
Si le premier élément de la colonne j est non nul, on passe directement à l’étape 2.

Dans le cas contraire, on cherche la première ligne R_x qui présente un élément j-ième non nul.

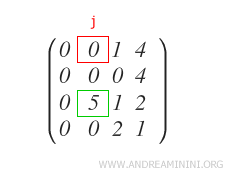
On échange ensuite la ligne R₁ avec la ligne R_x, puis l’on continue avec l’étape 2.

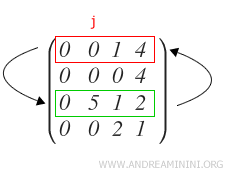
Remarque : La notation pour indiquer une permutation de lignes est la suivante :

On obtient ainsi le premier pivot (p₁) de la matrice.

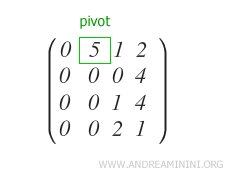
Étape 2

On doit ensuite annuler tous les autres éléments q_j-ièmes des lignes R_i situées sous le pivot.

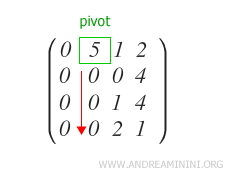
Si certains éléments restent non nuls, on soustrait de la ligne R_i un multiple approprié de la ligne du pivot.

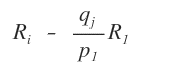
De cette manière, on élimine tout élément non nul situé sous le pivot.

Une fois arrivé à la dernière ligne, on passe à l’étape 3.

Étape 3

Chercher la première colonne j, placée à droite du dernier pivot, qui contienne un élément non nul dans les lignes inférieures.

Si une telle colonne n’existe pas, l’algorithme s’achève.

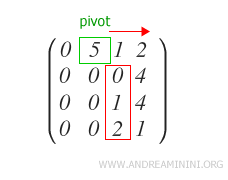
Dans notre cas, une telle colonne existe.

Le premier élément de cette colonne est nul. On cherche donc la première ligne inférieure avec un coefficient non nul, puis on permute les deux lignes correspondantes.

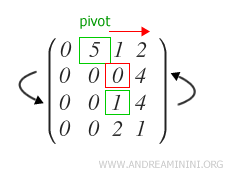
On obtient ainsi le deuxième pivot p₂ de la matrice échelonnée.

Si ce pivot se trouve sur la dernière ligne de la matrice (m), l’algorithme s’arrête ici.

Dans l’exemple illustré, nous sommes à la deuxième ligne (R₂) sur quatre : on poursuit donc avec l’étape 4.

Étape 4

Vérifier que tous les autres éléments q_j-ièmes des lignes R_i situées en dessous du dernier pivot p_k soient bien égaux à zéro.

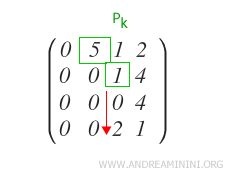
Dans cet exemple, on trouve un coefficient non nul dans la ligne R_i (i = 4).

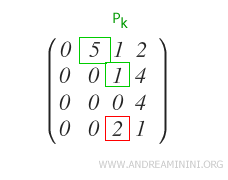
Pour l’éliminer, on soustrait de la ligne R_i un multiple adéquat de la ligne du pivot.

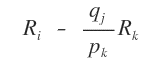
Cette opération doit être appliquée à tous les éléments de la ligne.

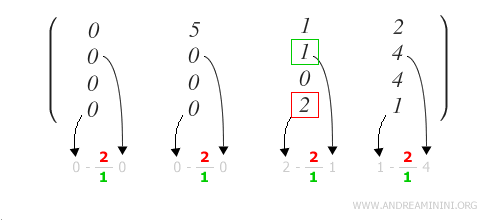
Remarque : Il n’est pas utile de l’appliquer aux premiers éléments de la ligne, car ils s’annulent automatiquement grâce aux zéros du pivot. Je les ai néanmoins affichés sur toute la ligne pour plus de lisibilité.

Après ces calculs, on obtient le résultat suivant :

La matrice est donc réduite à une forme échelonnée.

On poursuit ensuite le processus de la même façon.