Systèmes échelonnés d’équations linéaires
Un système d’équations linéaires est dit système échelonné (forme échelonnée ou echelon form) lorsqu’il peut être écrit sous la forme suivante :
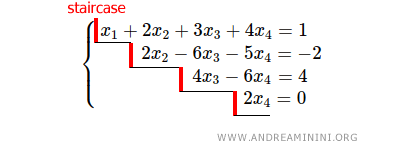
Le nombre d’inconnues présentes dans chaque équation diminue progressivement de la première à la dernière.
Le nombre d’échelons d’un système linéaire correspond exactement au rang de la matrice.
Cette forme rend le calcul du rang et la résolution du système beaucoup plus accessibles, même lorsqu’il comporte un grand nombre d’équations et d’inconnues.
Pourquoi les systèmes échelonnés sont-ils utiles ?
Les systèmes linéaires échelonnés se résoudent très facilement, car ils permettent de déterminer les inconnues pas à pas, en partant de la dernière équation et en remontant vers la première.
Lorsqu’un système n’est pas encore sous forme échelonnée, on peut le transformer à l’aide de la méthode de Gauss-Jordan.
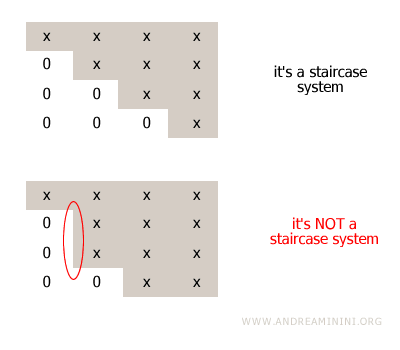
Remarque : Pour qu’un système soit considéré comme échelonné, chaque pivot doit apparaître exactement une ligne en dessous du pivot précédent. Si l’on saute deux lignes ou plus, la matrice n’est plus en forme échelonnée.
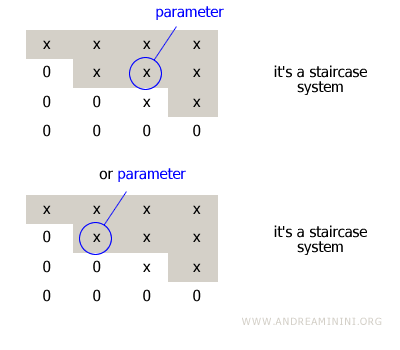
Si un échelon concerne deux variables (colonnes), l’une d’entre elles doit être considérée comme paramètre libre du système.
Exemple concret
Exemple 1
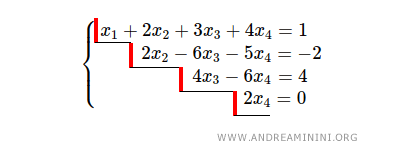
Considérons le système linéaire suivant, qui est déjà en forme échelonnée :
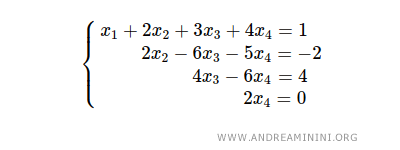
Il comporte 4 échelons et n = 4 inconnues.
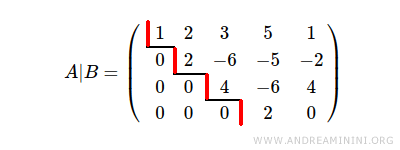
La matrice augmentée de ce système a pour rang r = 4, puisqu’on y trouve 4 échelons.
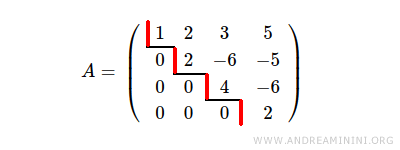
La matrice des coefficients présente elle aussi un rang égal à 4, pour la même raison.
D’après le théorème de Rouché-Capelli, le système admet donc au moins une solution.
Dans ce cas précis, la solution est unique, car le rang (r = 4) coïncide avec le nombre d’inconnues (n = 4).
$$ \infty^{n-r} = \infty^{4-4} = \infty^0 = 1 $$
On commence la résolution par la dernière équation, 2x4 = 0, qui se résout immédiatement : x4 = 0.
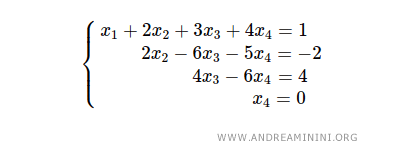
On remplace ensuite x4 = 0 dans la troisième équation, ce qui donne 4x3 = 4, donc x3 = 1.
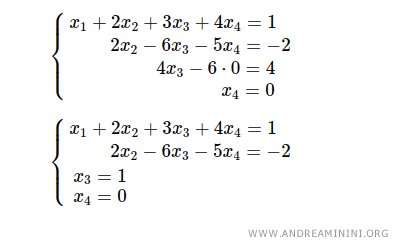
Puis, en insérant x3 = 1 et x4 = 0 dans la deuxième équation, on obtient : 2x2 - 6·1 - 5·0 = -2, d’où x2 = 2.
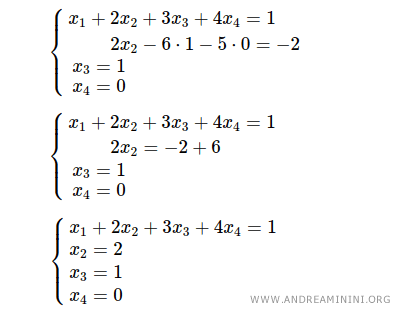
Enfin, en substituant x2 = 2, x3 = 1 et x4 = 0 dans la première équation, on obtient : x1 + 2·2 + 3·1 + 4·0 = 1, donc x1 = -6.
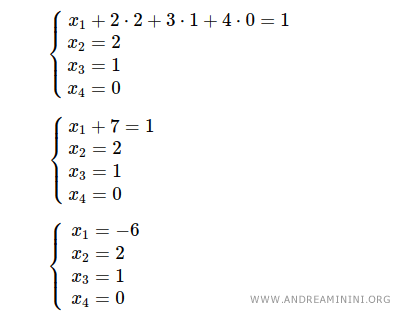
Le système est ainsi résolu en quelques étapes simples.
Les solutions sont : x1 = -6, x2 = 2, x3 = 1 et x4 = 0.
Remarque : C’est précisément l’intérêt de réécrire un système linéaire sous forme échelonnée : la procédure de résolution devient directe et beaucoup plus maniable, y compris pour des systèmes de grande taille.
Exemple 2
Considérons maintenant un autre système linéaire, lui aussi présenté sous forme échelonnée :
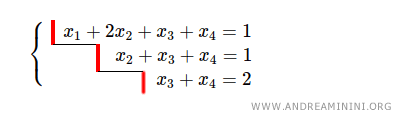
La matrice augmentée de ce système a pour rang r = 3, puisqu’elle comporte 3 échelons.
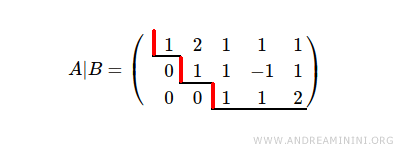
La matrice des coefficients a elle aussi un rang r = 3.
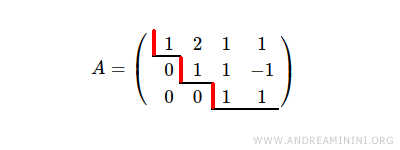
Le théorème de Rouché-Capelli indique alors que le système possède soit une solution unique, soit une infinité de solutions.
Dans ce cas, le système admet une infinité de solutions, car le rang (r = 3) est inférieur au nombre d’inconnues (n = 4).
$$ \infty^{n-r} = \infty^{4-3} = \infty^1 = \infty $$
Pour déterminer explicitement les solutions, il faut procéder à une paramétrisation du système.
Par exemple, à partir de la dernière équation, on peut exprimer la variable x3 en fonction de x4, choisi comme paramètre libre.
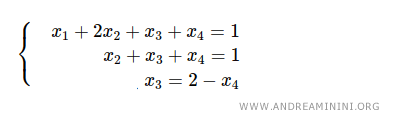
En remplaçant x3 = 2 - x4 dans la deuxième équation, on obtient x2 = -1.
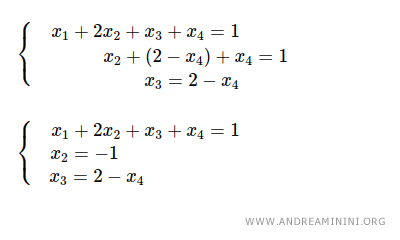
Enfin, en insérant x2 = -1 et x3 = 2 - x4 dans la première équation, on trouve : x1 = 1.
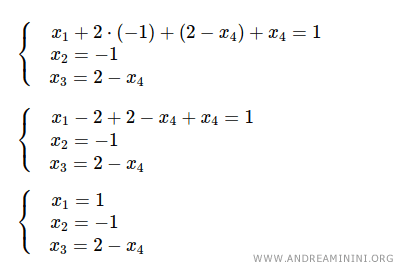
Les solutions du système s’expriment donc ainsi : x1 = 1, x2 = -1, x3 = 2 - x4, avec x4 comme paramètre libre k ∈ ℝ.
$$ \begin{cases} x_1 = 1 \\ x_2 = -1 \\ x_3 = 2 - k \end{cases} $$
Le système possède donc une infinité de solutions.
Remarques
Quelques points à retenir sur les systèmes linéaires échelonnés :
- Toute matrice échelonnée est une matrice triangulaire supérieure. En revanche, l’inverse n’est pas vrai : une matrice triangulaire supérieure n’est pas forcément échelonnée.
- Le déterminant d’une matrice carrée échelonnée est le produit des éléments de sa diagonale principale. Comme il s’agit d’une matrice triangulaire, tous les autres coefficients sont nuls, ce qui rend le calcul du déterminant particulièrement simple.
Et le même raisonnement peut être prolongé.