Matrice triangulaire supérieure
Une matrice carrée est dite triangulaire supérieure lorsque tous les éléments situés en dessous de la diagonale principale sont nuls : $$ \forall \ i > j, \ \ \ a_{ij} = 0 $$
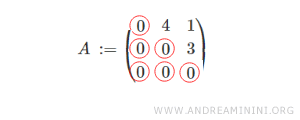
Exemple
Considérons une matrice d’ordre 3 (3 lignes et 3 colonnes) qui satisfait cette condition.
On constate que tous les coefficients placés sous la diagonale principale sont nuls.

Remarque : Les coefficients situés sur la diagonale, ainsi que la diagonale elle-même, peuvent être nuls ou non ; aucune contrainte particulière n’est imposée à ce sujet.
Si, en outre, tous les éléments de la diagonale principale sont nuls, on parle alors d’une matrice strictement triangulaire supérieure.
L’ensemble des matrices triangulaires supérieures à coefficients réels et d’ordre \( n \) se note généralement \( T^R \).
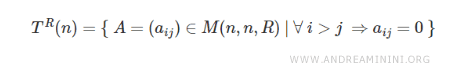
Intérêt des matrices triangulaires supérieures
Les matrices triangulaires supérieures occupent une place importante en algèbre linéaire, car elles permettent de simplifier de manière substantielle un grand nombre de calculs matriciels. Comme toute l’information pertinente est concentrée dans la partie supérieure de la matrice, le nombre d’opérations à effectuer ainsi que la complexité algorithmique sont considérablement réduits.
Une propriété fondamentale est que le déterminant d’une matrice triangulaire supérieure s’obtient directement comme le produit des coefficients de sa diagonale principale, les autres termes n’apportant aucune contribution.
Et ainsi de suite…