Propriétés du déterminant

Le déterminant d’une matrice présente un certain nombre de propriétés fondamentales :

1. Le déterminant de la matrice transposée, det(A^T), est toujours égal à celui de la matrice initiale, det(A).
   

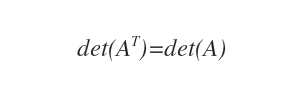
   Exemple. Dans la matrice suivante, l’opération de transposition ne modifie pas la valeur du déterminant.
   

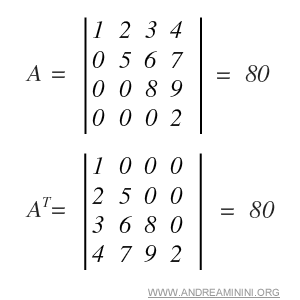
2. Lorsqu’une matrice est triangulaire (supérieure ou inférieure), son déterminant se calcule simplement comme le produit des éléments de la diagonale principale.
   

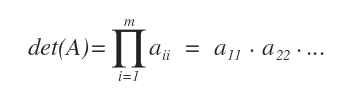
   Exemple. Dans ce cas de figure, le calcul du déterminant devient particulièrement direct et rapide.
   

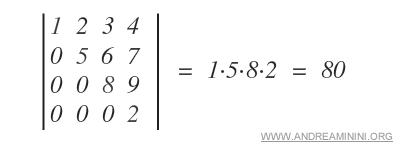
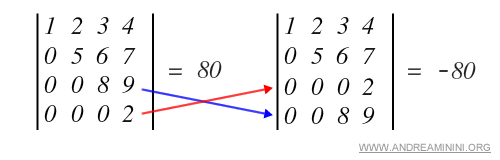
3. L’échange de deux lignes ou de deux colonnes inverse le signe du déterminant.

   Exemple.
   

4. Multiplier une ligne ou une colonne par un scalaire \( \alpha \) entraîne la multiplication du déterminant par ce même facteur : det(\(\alpha\)A) = \(\alpha\) det(A).
   

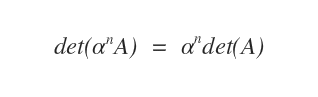
   Exemple. Ici, la quatrième ligne R₄ est multipliée par 2, ce qui a pour effet de doubler le déterminant.
   

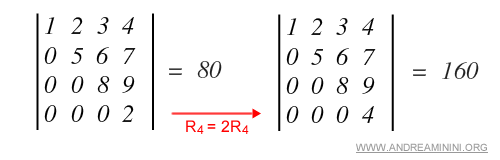
5. Ajouter à une ligne un multiple d’une autre (ou à une colonne un multiple d’une autre) ne modifie pas la valeur du déterminant.

   Exemple. Ici, la quatrième ligne R₄ est remplacée en lui additionnant deux fois la première ligne R₁.
   

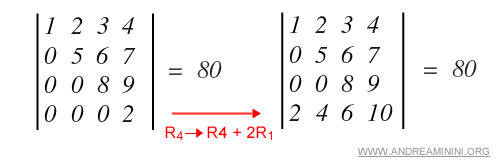
6. Le déterminant d’une matrice est nul dans les situations suivantes :
   
   a) Une ligne ou une colonne est entièrement composée de zéros.
   
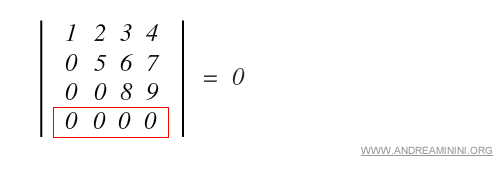
   b) Deux lignes ou deux colonnes sont identiques.
   
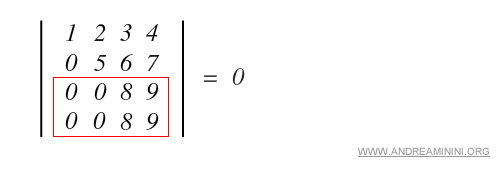
   c) Deux lignes ou deux colonnes sont proportionnelles.
   

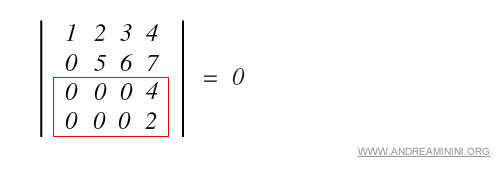
   Remarque. Lorsqu’une ligne ou une colonne peut s’exprimer comme une combinaison linéaire des autres, la matrice est dite linéairement dépendante, et son déterminant est nul.

7. Le déterminant du produit de deux matrices vérifie l’identité : det(AB) = det(A) det(B) ( Théorème de Binet ).
   
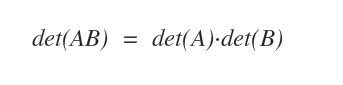
8. Le déterminant de l’inverse d’une matrice est égal à l’inverse de son déterminant : det(A^-1) = 1/det(A).
   

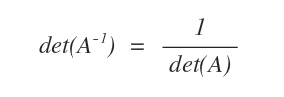
   Démonstration. Selon le théorème de Binet, le déterminant d’un produit A·B est égal au produit de leurs déterminants : $$ det(A \cdot B) = det(A) \cdot det(B) $$ Appliquons cela à une matrice A inversible et à son inverse A^-1 : $$ det(A \cdot A^{-1}) = det(A^{-1}) \cdot det(A) $$ Comme le produit d’une matrice par son inverse donne la matrice identité, on obtient : $$ det(A \cdot A^{-1}) = det(I) $$ Le déterminant de la matrice identité vaut 1 ; par conséquent : $$ det(A) \cdot det(A^{-1}) = 1 $$ D’où : $$ det(A^{-1}) = \frac{1}{det(A)} $$ La propriété est ainsi démontrée.

Et ainsi de suite.