Vecteurs orthogonaux

Deux vecteurs sont dits orthogonaux lorsqu’ils satisfont la propriété d’orthogonalité, c’est-à-dire lorsqu’ils sont perpendiculaires l’un à l’autre.

Dans un espace vectoriel réel, deux vecteurs v₁ et v₂ sont orthogonaux si leur produit scalaire est nul : $$ \langle v_1,v_2 \rangle = 0 $$

L’orthogonalité entre deux vecteurs se note à l’aide du symbole de la T inversée :

$$ v_1 \perp v_2 $$

Remarque : Le produit scalaire nul est une condition nécessaire, mais non suffisante, pour garantir l’orthogonalité. Il faut en outre que les deux vecteurs ne soient pas le vecteur nul, c’est-à-dire qu’ils aient une norme strictement positive. Par exemple, le produit scalaire de n’importe quel vecteur avec le vecteur nul est nul, mais dans ce cas on ne parle pas d’orthogonalité. $$ \langle \vec{v} , \vec{0} \rangle = 0 $$

Exemple de vecteurs orthogonaux

Dans l’espace vectoriel V = ℝ² défini sur le corps K = ℝ, considérons les vecteurs suivants :

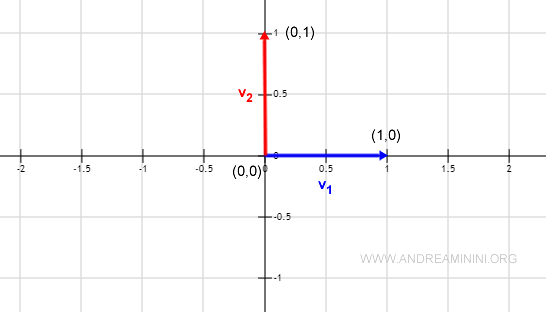
$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$

Le produit scalaire euclidien <v₁, v₂> est nul :

$$ \langle v_1,v_2 \rangle = 1\cdot0 + 0\cdot1 = 0 $$

Ces deux vecteurs sont donc orthogonaux.

Remarque : Placés dans le plan cartésien en prenant pour origine O(0,0), ces vecteurs apparaissent clairement comme deux directions perpendiculaires.

 

Exemple 2

Considérons maintenant un autre couple de vecteurs :

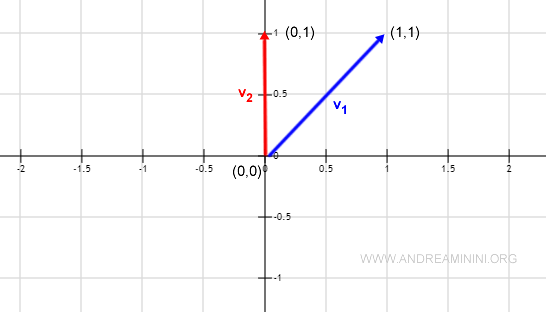
$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$

Leur produit scalaire n’est pas nul :

$$ \langle v_1,v_2 \rangle = 1\cdot0 + 1\cdot1 = 1 $$

Ces vecteurs ne sont donc pas orthogonaux.

Remarque : La représentation graphique dans le plan cartésien met en évidence que ces vecteurs ne sont pas perpendiculaires.

 

Cosinus de l’angle et orthogonalité

Si les deux vecteurs sont non nuls, il existe une relation directe entre le cosinus de l’angle qu’ils forment, leur produit scalaire et leurs normes :

$$ \cos(v_1,v_2) = \frac{ \langle v_1,v_2 \rangle } { ||v_1|| \cdot ||v_2|| } $$

Par convention, si l’un des deux vecteurs est nul, on définit le cosinus comme étant nul :

$$ \cos(v_1,v_2) := 0 \:\: \text{si} \:\: v_1=0_V \:\: \text{ou} \:\: v_2=0_V $$

Exemple pratique

Calculons le cosinus de l’angle entre les vecteurs :

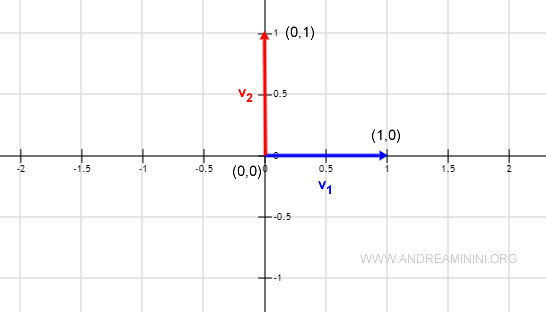
$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$

Leur produit scalaire vaut :

$$ \langle v_1,v_2 \rangle = 1\cdot0 + 0\cdot1 = 0 $$

Les normes respectives sont :

$$ ||v_1|| = \sqrt{1^2+0^2} = 1 \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$

D’où :

$$ \cos(v_1,v_2) = \frac{ 0 }{ 1 } = 0 $$

L’angle entre les deux vecteurs est bien de 90°, et son cosinus est nul.

Exemple 2

Calculons maintenant le cosinus pour un autre couple de vecteurs :

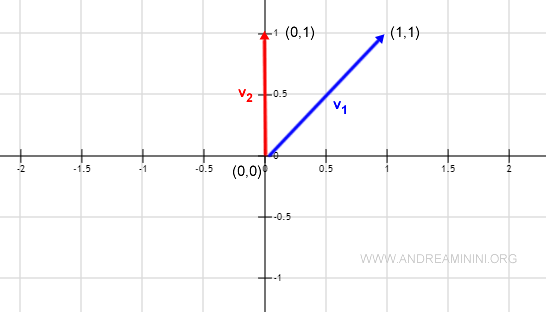
$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$

Le produit scalaire est :

$$ \langle v_1,v_2 \rangle = 1\cdot0 + 1\cdot1 = 1 $$

Leurs normes respectives sont :

$$ ||v_1|| = \sqrt{1^2+1^2} = \sqrt{2} \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$

Le cosinus de l’angle vaut donc :

$$ \cos(v_1,v_2) = \frac { 1 } { \sqrt{2} \cdot 1 } = \frac {1} { \sqrt{2} } $$

Autrement dit, les deux vecteurs forment un angle de 45°.

Différence entre perpendicularité et orthogonalité

Les termes « orthogonalité » et « perpendicularité » sont le plus souvent employés comme synonymes.

Cependant, on réserve généralement « perpendicularité » au contexte géométrique, tandis que le terme « orthogonalité » s’étend à des domaines plus généraux, comme l’algèbre linéaire ou l’analyse fonctionnelle.

Bases orthogonales et orthonormées

Les vecteurs orthogonaux permettent de construire des bases orthogonales et des bases orthonormées :

• Une base orthogonale est formée de vecteurs deux à deux orthogonaux.
• Une base orthonormée est une base orthogonale dont tous les vecteurs ont, en outre, une norme unitaire.