Complément orthogonal

Le complément orthogonal (ou supplément orthogonal) d’un sous-espace vectoriel W de V est le sous-espace W* formé de tous les vecteurs de V qui sont orthogonaux à chacun des vecteurs de W.

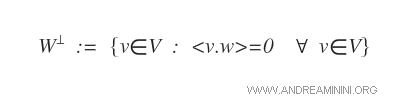
On le note généralement à l’aide du symbole T inversé.

Dans un espace vectoriel V de dimension finie, les sous-espaces W et W* sont supplémentaires.

Autrement dit, leur somme directe reconstitue l’espace vectoriel tout entier : $$ V = W \oplus W^* $$

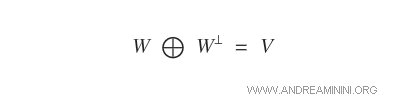
Détermination des vecteurs du complément orthogonal

Un vecteur v ∈ V appartient à W* si, et seulement si, il est orthogonal à tous les éléments de la base B_W = { w₁, …, wₙ } du sous-espace W.

Cela revient à résoudre le système d’équations cartésiennes suivant :

$$ \begin{cases} <v,w_1> = c_{11} v_1 + \ldots + c_{1n} v_n = 0 \\ <v,w_2> = c_{21} v_1 + \ldots + c_{2n} v_n = 0 \\ ⋮ \\ <v,w_k> = c_{k1} v_1 + \ldots + c_{kn} v_n = 0 \end{cases} $$

Les coefficients c correspondent aux composantes des vecteurs w de la base de W :

$$ W = B \{ w_1, w_2, \ldots, w_k \} $$

Le vecteur v est donc un vecteur générique de V, qui peut ou non appartenir à W*.

Remarque. Le système est homogène : pour qu’un vecteur v soit orthogonal à un vecteur w, leur produit scalaire doit nécessairement être nul.

Exemple de calcul

Dans l’espace vectoriel V = R⁴ sur le corps K = R, considérons le sous-espace W engendré par la base suivante :

$$ B_W = \{ w_1, w_2 \} \\ w_1 = (1,1,1,1) \\ w_2 = (1,0,1,0) $$

Nous cherchons les vecteurs v ∈ V qui sont orthogonaux aux deux vecteurs de B.

$$ v = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} $$

Le système associé est alors :

$$ \begin{cases} x_1 + x_2 + x_3 + x_4 = 0 \\ x_1 + x_3 = 0 \end{cases} $$

Ce système se réécrit :

$$ \begin{cases} x_2 + x_4 = 0 \\ x_1 = -x_3 \end{cases} $$

On obtient donc :

$$ \begin{cases} x_2 = -x_4 \\ x_1 = -x_3 \end{cases} $$

Il en résulte que les vecteurs qui engendrent la base du complément orthogonal W* sont :

$$ v = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} = B_{W*} \left\{ \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix}, \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} \right\} $$

Ainsi, tout vecteur engendré par cette base appartient à W*.

Exemple. Le vecteur v = (3,2,-3,-2) appartient bien au complément orthogonal, puisqu’il s’exprime comme combinaison linéaire des vecteurs de la base de W* : $$ v = \begin{pmatrix} 3 \\ 2 \\ -3 \\ -2 \end{pmatrix} = 2 \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix} + 3 \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} $$