Base orthonormée
Une base orthonormée d’un espace vectoriel B{v,w} est un ensemble de vecteurs orthogonaux $$ \langle v,w\rangle =0 \:\: \text{si} \:\: v \ne w $$ dont chacun possède une norme unitaire : $$ || \vec{v} || = || \vec{w} || = 1 $$
En d’autres termes, une base orthonormée doit satisfaire deux conditions fondamentales :
- Chaque vecteur de la base est de norme unitaire, c’est-à-dire de longueur exactement égale à 1.
- Les vecteurs, distincts deux à deux, sont orthogonaux ; par conséquent, leur produit scalaire <v,w> est nul.
Remarque. Les vecteurs d’une base orthonormée sont également appelés vecteurs unitaires, car la norme de chacun vaut 1 : $$ ||v|| = 1 $$ $$ ||w|| = 1 $$ Cette propriété découle du fait que le produit scalaire <v,w> = 1 lorsque v = w. La norme induite par le produit scalaire se définit ainsi : $$ ||v|| = \sqrt{ \langle v,v \rangle } $$ Ainsi, si v = w, il est nécessaire que <v,w> = 1 pour que la norme soit unitaire.
Exemple de base orthonormée
L’ensemble suivant constitue un exemple classique de base orthonormée.
Il s’agit de la base canonique du plan :
$$ B = \{ \vec{v_1} , \vec{v_2} \} = \left\{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right\} $$
Chacun de ces vecteurs est de norme unitaire :
$$ ||\vec{v}|| = \sqrt{1^2+0^2} = 1 $$
$$ ||\vec{w}|| = \sqrt{0^2+1^2} = 1 $$
De plus, ils sont distincts et leur produit scalaire est nul :
$$ \langle v,w\rangle = ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0 $$
Ils forment donc une base orthonormée.
Graphiquement, ces deux vecteurs sont perpendiculaires (angle de 90°) et de longueur égale à 1.
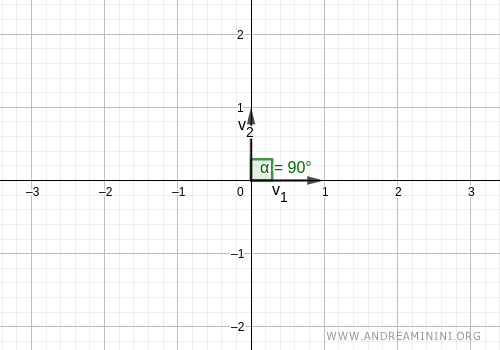
Remarque. Dans une base orthonormée, les vecteurs sont des vecteurs unitaires. C’est une autre manière de vérifier l’orthonormalité de la base : $$ ||v|| = \sqrt{1^2+0^2} = 1 $$ $$ ||w|| = \sqrt{0^2+1^2} = 1 $$
Différence entre bases orthogonales et bases orthonormées
Toute base orthonormée est une base orthogonale, puisque ses vecteurs sont orthogonaux entre eux.
Inversement, toute base orthogonale n’est pas nécessairement orthonormée.
Exemple
L’ensemble suivant constitue une base orthogonale :
$$ B = \left\{ \begin{pmatrix} 1 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 1 \end{pmatrix} \right\} $$
Il s’agit de deux vecteurs distincts dont le produit scalaire est nul :
$$ \langle v,w\rangle = ( 1 \cdot 1 ) + ( -1 \cdot 1 ) = 1-1 = 0 $$
Ils forment donc un angle droit et sont orthogonaux.
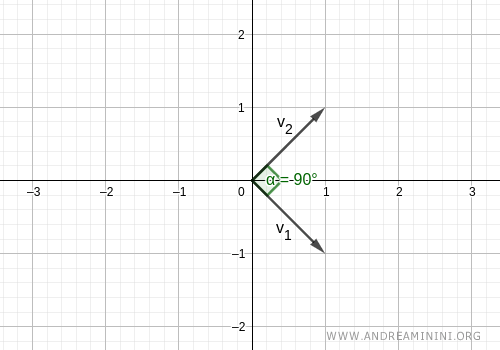
Cependant, cette base n’est pas orthonormée, car ses vecteurs n’ont pas de norme unitaire :
$$ ||v_1|| = \sqrt{1^2+(-1)^2} = \sqrt{2} $$ $$ ||v_2|| = \sqrt{1^2+1^2} = \sqrt{2} $$
Autrement dit, leur longueur est différente de 1.
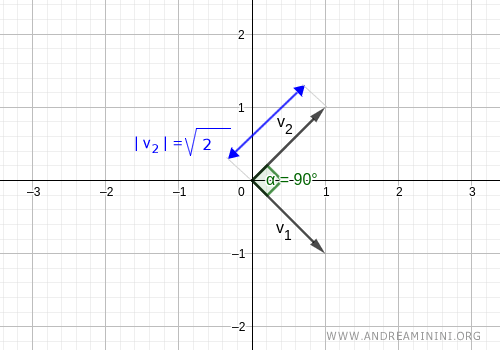
Ainsi, bien que les vecteurs soient orthogonaux, ils ne forment pas une base orthonormée.
Remarque. Toute base orthogonale peut être transformée en base orthonormée en normalisant ses vecteurs. Pour plus de détails, voir comment transformer une base orthogonale en base orthonormée.