Bases orthogonales

Dans un espace vectoriel B{v,w}, une base orthogonale est constituée de vecteurs orthogonaux. Autrement dit, le produit scalaire de toute paire de vecteurs distincts est nul : $$ \langle v,w\rangle =0 \:\:\:\: \forall \ v,w $$

Cette condition d’orthogonalité doit être vérifiée pour chaque paire de vecteurs de la base.

Exemple de base orthogonale

L’ensemble suivant constitue un exemple simple de base orthogonale, formée de deux vecteurs perpendiculaires :

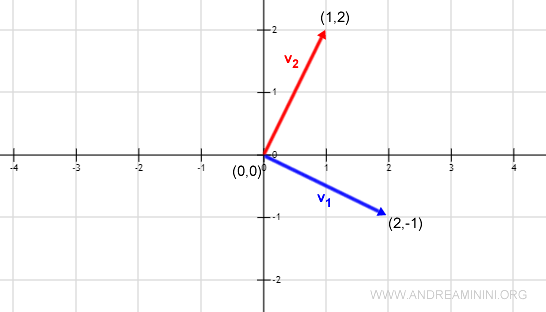
$$ B = \{ \begin{pmatrix} 2 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \end{pmatrix} \} $$

$$ \langle v_1,v_2\rangle = 2\cdot1 + (-1)\cdot2 = 2 - 2 = 0 $$

Remarque. La représentation graphique de ces vecteurs dans le plan montre immédiatement leur caractère perpendiculaire.

Différence entre bases orthogonales et bases orthonormées

Une base orthogonale devient une base orthonormée lorsque ses vecteurs, en plus d’être orthogonaux, sont de norme unitaire. Autrement dit, le produit scalaire d’un vecteur avec lui-même vaut 1, tandis que celui de deux vecteurs distincts vaut 0.

Exemple

L’ensemble suivant est à la fois une base orthogonale et une base orthonormée :

$$ B = \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \} $$

Le produit scalaire de deux vecteurs distincts est nul :

$$ \langle v,w\rangle = ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0 $$

Le produit scalaire d’un vecteur avec lui-même vaut 1 :

$$ \langle v,v\rangle = ( 1 \cdot 1 ) + ( 0 \cdot 0 ) = 1 $$

$$ \langle w,w\rangle = ( 0 \cdot 0 ) + ( 1 \cdot 1 ) = 1 $$

De l’orthogonalité à l’orthonormalité

Toute base orthogonale peut être transformée en base orthonormée en normalisant ses vecteurs, c’est-à-dire en divisant chacun d’eux par sa norme.

Remarque. Pour plus de précisions, voir la procédure de transformation d’une base orthogonale en base orthonormée.