Dépendance et indépendance linéaire de vecteurs

Soient m vecteurs v₁, v₂, ..., v_m dans un espace vectoriel V défini sur un corps K. Ces vecteurs sont dits linéairement indépendants lorsque la seule combinaison linéaire donnant le vecteur nul est la combinaison triviale : $$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 + \ ... \ + \alpha_m \cdot \vec{v}_m = \vec{0} $$ À l’inverse, s’il existe des solutions non triviales, les vecteurs sont linéairement dépendants.

Une combinaison linéaire est dite triviale lorsque tous les coefficients sont nuls :

$$ a_1 = a_2 = \ ... = \ a_m = 0 $$

Dès qu’au moins un coefficient est non nul, la combinaison est qualifiée de non triviale.

Vecteurs linéairement indépendants

Dans un espace vectoriel V sur un corps K, les vecteurs v₁,...,v_m ∈ V sont linéairement indépendants si aucune combinaison linéaire ne conduit au vecteur nul, hormis la combinaison triviale : $$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0}, \ \ \ \ \ \ \alpha \in K $$

Qu’appelle-t-on combinaison linéaire triviale ?

C’est celle pour laquelle tous les coefficients sont nuls : { a₁=0, ..., a_m=0 }.

Pourquoi exclure la combinaison triviale ?

Parce que toute combinaison où les coefficients sont nuls produit nécessairement le vecteur nul : $$ 0 \cdot v_1 + ... + 0 \cdot v_m = 0 $$ Cette solution, présente dans tous les cas, ne permet donc pas de distinguer indépendance et dépendance linéaire.

Vecteurs linéairement dépendants

Dans un espace vectoriel V sur un corps K, les vecteurs v₁,...,v_m ∈ V sont linéairement dépendants dès qu’il existe au moins une combinaison linéaire non triviale qui donne le vecteur nul : $$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0}, \ \ \ \ \ \ \alpha \in K $$

La solution triviale est exclue, puisqu’elle apparaît toujours et n’apporte aucune information. Dans ce cas, au moins un des coefficients est non nul.

On obtient alors le théorème suivant :

Les vecteurs v₁,...,v_m sont linéairement dépendants si l’un d’eux (par exemple v₁) peut s’exprimer comme combinaison linéaire des autres :

$$ v_1 = \beta_2 \cdot v_2 + ... + \beta_m \cdot v_m $$ $$ avec \ \beta_2, ..., \beta_m \in R $$

Ce théorème ne précise pas quel vecteur peut être écrit comme combinaison des autres ; il affirme seulement qu’un tel vecteur existe lorsque les vecteurs sont dépendants. Autrement dit, n’importe lequel parmi v₁,...,v_m peut jouer ce rôle.

Interprétation géométrique

Dans le plan \( \mathbb{R}^2 \), deux vecteurs sont linéairement dépendants lorsqu’ils sont parallèles ou confondus, c’est-à-dire lorsqu’ils appartiennent à une même droite et partagent la même direction.

Dans l’espace \( \mathbb{R}^3 \), trois vecteurs sont linéairement dépendants s’ils sont contenus dans un même plan.

Remarque. Ces observations géométriques ne valent que pour les espaces de dimension 2 ou 3 (R² et R³). Elles ne se généralisent pas à des espaces de dimension supérieure tels que R⁴, R⁵, etc.

Un exemple pratique

Exemple 1

Considérons deux vecteurs de l’espace vectoriel \( V = \mathbb{R}^2 \), défini sur le corps des réels \( K = \mathbb{R} \) :

$$ \vec{v}_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix}, \qquad \vec{v}_2 = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$

Étudions la combinaison linéaire suivante :

$$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 = \vec{0} $$

Autrement dit :

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ 5 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

On obtient alors le système :

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ a_1 + 5a_2 = 0 \end{cases} $$

En isolant \( a_1 \) dans la seconde équation, on a \( a_1 = -5a_2 \). Le système devient :

$$ \begin{cases} 3(-5a_2) + 2a_2 = 0 \\ a_1 = -5a_2 \end{cases} $$

soit

$$ \begin{cases} -13a_2 = 0 \\ a_1 = -5a_2 \end{cases} $$

d’où \( a_1 = a_2 = 0 \). La seule solution est donc triviale, ce qui prouve que \( v_1 \) et \( v_2 \) sont linéairement indépendants.

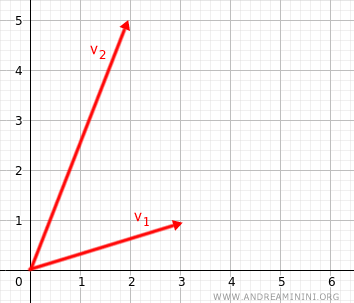
Remarque. Dans le plan \( \mathbb{R}^2 \), deux vecteurs sont linéairement dépendants uniquement lorsqu’ils sont parallèles. Ainsi, s’ils sont indépendants, ils ne peuvent pas être parallèles. Cette propriété est spécifique au plan et ne se transpose pas à des espaces de dimension supérieure.

Exemple 2

Considérons maintenant trois vecteurs de \( V = \mathbb{R}^2 \) :

$$ \vec{v}_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix}, \quad \vec{v}_2 = \begin{pmatrix} 1 \\ 4 \end{pmatrix}, \quad \vec{v}_3 = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$

On cherche à savoir si ces vecteurs sont indépendants. Le système associé est :

$$ \begin{cases} 3a_1 + a_2 + 2a_3 = 0 \\ a_1 + 4a_2 + a_3 = 0 \end{cases} $$

Ce système comporte trois inconnues mais seulement deux équations. D’après le théorème de Rouché-Capelli, il admet une infinité de solutions, dont certaines non triviales.

Les trois vecteurs sont donc linéairement dépendants : l’un d’entre eux peut s’exprimer comme combinaison linéaire des deux autres.

Exemple 3

Dans \( V = \mathbb{R}^3 \), considérons :

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}, \qquad v_2 = \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} $$

Le système associé est :

$$ \begin{cases} \alpha_1 + 3\alpha_2 = 0 \\ 2\alpha_1 + 2\alpha_2 = 0 \\ -\alpha_1 + 3\alpha_2 = 0 \end{cases} $$

Sa résolution montre que la seule solution est triviale : \( \alpha_1 = \alpha_2 = 0 \). Ainsi, \( v_1 \) et \( v_2 \) sont linéairement indépendants.

Exemple 4

Dans le même espace, prenons :

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}, \qquad v_2 = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} $$

Le système associé devient :

$$ \begin{cases} \alpha_1 + 3\alpha_2 = 0 \\ 2\alpha_1 + 6\alpha_2 = 0 \\ -\alpha_1 + 3\alpha_2 = 0 \end{cases} $$

Celui-ci admet des solutions non triviales. On en conclut que \( v_1 \) et \( v_2 \) sont linéairement dépendants.

Exemple 5

Considérons trois vecteurs de l’espace vectoriel \( V = \mathbb{R}^3 \) :

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix}, \qquad v_2 = \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix}, \qquad v_3 = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

On cherche à déterminer s’ils sont indépendants en étudiant la combinaison linéaire :

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

c’est-à-dire :

$$ \begin{pmatrix} 3a_1 \\ a_1 \\ -2a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ -a_2 \\ 0 \end{pmatrix} + \begin{pmatrix} a_3 \\ -3a_3 \\ 2a_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Ce calcul conduit au système suivant :

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ -2a_1 + 2a_3 = 0 \end{cases} $$

La troisième équation donne immédiatement \( a_1 = a_3 \). En reportant dans les deux autres, on obtient :

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ -a_2 - 2a_3 = 0 \\ a_1 = a_3 \end{cases} $$

La deuxième équation fournit \( a_2 = -2a_3 \). Le système devient alors :

$$ \begin{cases} 4a_3 + 2(-2a_3) = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

soit simplement :

$$ \begin{cases} 0 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

Le système admet donc une infinité de solutions, puisque \( a_3 \) est libre et fixe les valeurs de \( a_1 \) et \( a_2 \). On en conclut que \( v_1, v_2 \) et \( v_3 \) sont linéairement dépendants.

En d’autres termes, l’un des trois vecteurs peut s’exprimer comme combinaison linéaire des deux autres.

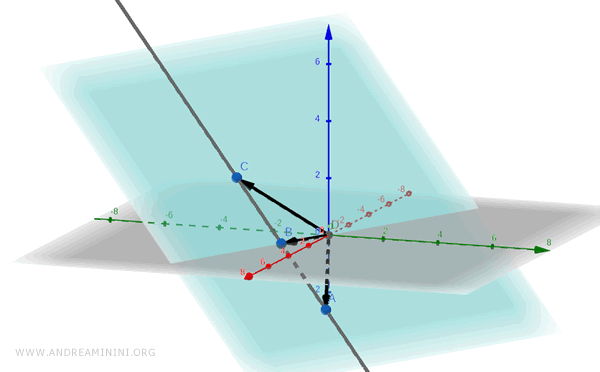
Remarque. On vérifie par exemple que $$ v_1 = 2v_2 - v_3, \quad \text{c’est-à-dire } \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = 2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} - \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix}. $$

Géométriquement, cela signifie que les trois vecteurs \( v_1, v_2, v_3 \) appartiennent à un même plan de l’espace tridimensionnel.

 

La démonstration

Un ensemble de vecteurs \( v_1,\dots,v_m \) est linéairement dépendant s’il existe une combinaison linéaire égale au vecteur nul, où les coefficients scalaires \( \alpha_1,\dots,\alpha_m \) ne sont pas tous nuls :

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} $$

Supposons que \( \alpha_1 \neq 0 \). On peut alors écrire :

$$ \alpha_1 \cdot \vec{v}_1 = - \alpha_2 \cdot \vec{v}_2 - ... - \alpha_m \cdot \vec{v}_m $$

et en divisant par \( \alpha_1 \) :

$$ \vec{v}_1 = - \frac{\alpha_2}{\alpha_1} \cdot \vec{v}_2 - ... - \frac{\alpha_m}{\alpha_1} \cdot \vec{v}_m $$

En posant :

$$ \beta_j = - \frac{\alpha_j}{\alpha_1}, \qquad j=2,\dots,m $$

on obtient la relation souhaitée :

$$ \vec{v}_1 = \beta_2 \cdot \vec{v}_2 + ... + \beta_m \cdot \vec{v}_m $$

Remarque. Les coefficients \( \beta_j \) correspondent simplement aux rapports \(-\alpha_j / \alpha_1\).

La réciproque est immédiate : si un vecteur, par exemple \( v_1 \), peut s’écrire comme combinaison linéaire des autres :

$$ \vec{v}_1 = \beta_2 \cdot \vec{v}_2 + ... + \beta_m \cdot \vec{v}_m $$

alors les vecteurs \( v_1, v_2, \dots, v_m \) sont dépendants, car :

$$ -\vec{v}_1 + \beta_2 \cdot \vec{v}_2 + ... + \beta_m \cdot \vec{v}_m = \vec{0} $$

La combinaison n’est pas triviale, puisque le coefficient de \( v_1 \) vaut \(-1\), donc non nul. La dépendance linéaire est ainsi établie.

Corollaire 1

Si les vecteurs v₁,...,v_m sont linéairement dépendants, alors tout sous-ensemble de ces vecteurs l’est également.

Démonstration

Partons de l’hypothèse \( \alpha_1 = 1 \).

La combinaison linéaire suivante est donc non triviale, ce qui établit la dépendance des vecteurs :

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} $$

Si l’on suppose \( \alpha_m = 0 \), le dernier terme disparaît :

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_{m-1} \cdot \vec{v}_{m-1} = \vec{0} $$

Comme \( \alpha_1 \neq 0 \), cette combinaison reste non triviale. Le sous-ensemble correspondant est donc lui aussi linéairement dépendant.

Corollaire 2

Si les vecteurs v₁,...,v_m sont linéairement dépendants, alors tout ensemble élargi { v₁,...,v_m+k } l’est également, en posant \( \alpha_{m+1} = ... = \alpha_{m+k} = 0 \).

Démonstration

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m + ( \alpha_{m+1} \cdot \vec{v}_{m+1} + ... + \alpha_{m+k} \cdot \vec{v}_{m+k} ) = \vec{0} $$

avec \( \alpha_{m+1} = ... = \alpha_{m+k} = 0 \).

On retrouve donc :

$$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} $$

La combinaison initiale étant déjà non triviale, la nouvelle l’est tout autant. Ainsi, l’ensemble élargi est nécessairement linéairement dépendant.

Déterminer la dépendance linéaire par le rang d’une matrice

Pour savoir si un ensemble de vecteurs numériques est dépendant ou indépendant, on peut utiliser le rang de la matrice associée.

Un ensemble de n vecteurs v₁, ..., v_n est linéairement indépendant si le rang par lignes de la matrice \( M_{m,n}(\mathbb{R}) \) est égal à n : $$ r_k = n $$

Le rang par colonnes correspond au nombre maximal de colonnes linéairement indépendantes, celles-ci étant vues comme des vecteurs à n composantes.

• Si \( r_k = n \), les colonnes sont indépendantes.
• Si \( r_k < n \), les colonnes sont dépendantes.

Dans le cas où \( r_k < n \), on peut identifier un sous-ensemble de vecteurs indépendants grâce aux mineurs complémentaires non nuls.

Les vecteurs qui apparaissent dans un mineur complémentaire de déterminant non nul sont nécessairement indépendants.

Remarque. Ce principe reste valable si l’on considère les lignes plutôt que les colonnes, puisque pour toute matrice \( M_{m,n}(\mathbb{R}) \) le rang par lignes coïncide avec le rang par colonnes.

Un exemple concret

Dans l’espace vectoriel \( V = \mathbb{R}^4 \), défini sur \( K = \mathbb{R} \), considérons :

$$ v_1 = ( 1, 0, 1, 2 ), \quad v_2 = ( 1, 3, 0, 0 ), \quad v_3 = ( 1, -3, 2, 4 ), \quad v_4 = ( 2, 3, 1, 2 ) $$

On les dispose comme colonnes d’une matrice carrée \( 4 \times 4 \) :

$$ M_{4,4} = \begin{bmatrix} 1 & 0 & 1 & 2 \\ 1 & 3 & 0 & 0 \\ 1 & -3 & 2 & 4 \\ 2 & 3 & 1 & 2 \end{bmatrix} $$

Son déterminant est nul :

$$ \Delta M = 0 $$

Le rang est donc strictement inférieur à 4.

Pour le préciser, on applique le théorème des mineurs complémentaires. Un mineur d’ordre 2 étant non nul :

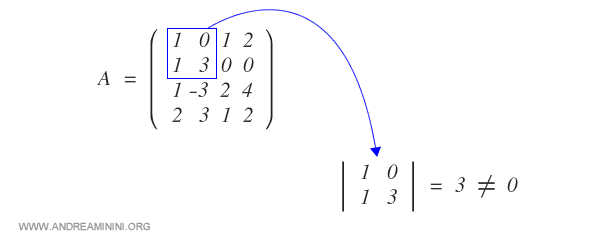
la matrice est au moins de rang 2.

On vérifie ensuite les mineurs d’ordre 3 :

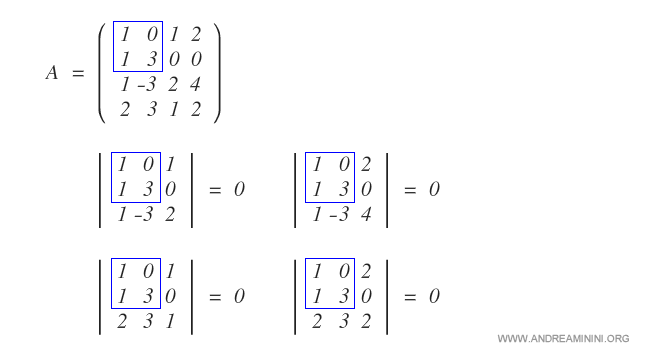
Tous étant nuls, le rang ne peut être 3 ni supérieur. On conclut que le rang de la matrice est 2.

Dès lors, comme la matrice comporte n = 4 colonnes mais seulement r_k = 2, on a :

$$ r_k \neq n $$

Selon le critère :

1. Si \( r_k = n \), les vecteurs sont indépendants.
2. Si \( r_k \neq n \), ils sont dépendants.

Il en résulte que les vecteurs v₁, v₂, v₃ et v₄ sont linéairement dépendants.

Comment identifier les vecteurs indépendants ?

Il suffit de retenir les vecteurs qui apparaissent dans des mineurs complémentaires de déterminant non nul. Par exemple, v₁ et v₂ sont indépendants car ils appartiennent à un mineur dont le déterminant est non nul :

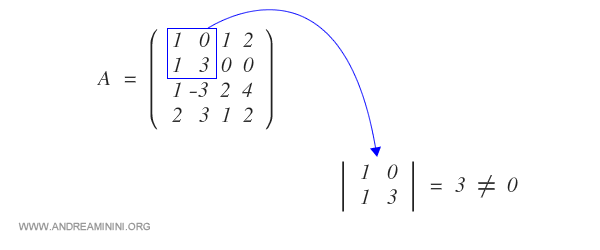
Ici, le rang (2) correspond bien au nombre de colonnes du mineur.

On peut de la même manière vérifier l’indépendance de couples tels que (v₂, v₃), (v₃, v₄), (v₂, v₄), (v₁, v₃) ou (v₁, v₄).

L’algorithme d’élimination de Gauss

La dépendance linéaire d’un ensemble de vecteurs peut aussi être étudiée à partir du rang de la matrice qui les représente, rang que l’on calcule à l’aide de l’algorithme d’élimination de Gauss-Jordan.

Dans cette méthode, le nombre de pivots obtenus correspond directement au rang de la matrice.

Exemple

Reprenons l’exercice précédent, où les quatre vecteurs sont disposés en colonnes dans une matrice \( 4 \times 4 \) :

$$ M_{4,4} = \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 3 & -3 & 3 \\ 1 & 0 & 2 & 1 \\ 2 & 0 & 4 & 2 \end{bmatrix} $$

On réduit ensuite cette matrice en forme échelonnée en appliquant les opérations élémentaires de Gauss :

$$ M_{4,4} = \begin{bmatrix} 1 & 0 & 2 & 1 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} $$

Remarque. Pour alléger l’exposé, on n’indique pas ici toutes les étapes intermédiaires de la réduction de Gauss-Jordan. Pour consulter le développement complet, cliquez ici.

La matrice présente deux pivots, d’où un rang \( r_k = 2 \).

Il s’ensuit que les vecteurs v₁, v₂, v₃ et v₄ sont linéairement dépendants, puisque \( r_k < n \).

En revanche, les vecteurs v₁ et v₂, correspondant aux colonnes portant les pivots, sont indépendants entre eux.

Remarque. La forme échelonnée ne sert qu’au calcul du rang. Les vecteurs d’origine restent inchangés : \( v_1 = (1,1,1,2), \; v_2 = (0,3,-3,3), \; v_3 = (1,0,2,1), \; v_4 = (2,0,4,2) \).

Théorèmes sur l’indépendance linéaire

• Si un ensemble \( \{v_1, v_2, ..., v_n\} \) est linéairement indépendant, aucun de ces vecteurs ne peut être nul : $$ \vec{v}_1 \ne \vec{0}, \quad \vec{v}_2 \ne \vec{0}, \quad \dots, \quad \vec{v}_n \ne \vec{0} $$

  Voir la démonstration.

• Dans un espace vectoriel de dimension finie \( V \), si \( \{ v_1, v_2, ..., v_n \} \) est un système générateur et \( \{ w_1, w_2, ..., w_p \} \) un ensemble de vecteurs linéairement indépendants de \( V \), alors : $$ p \le n $$

  Autrement dit, le nombre de vecteurs indépendants de \( V \) ne peut dépasser celui d’un système générateur.
  
  Voir la démonstration.

Observations

Quelques remarques utiles à propos de la dépendance et de l’indépendance linéaire :

• Le vecteur nul est toujours dépendant
  Par définition, un vecteur est dit indépendant si le seul moyen d’obtenir le vecteur nul est la combinaison triviale (\( \alpha = 0 \)) : $$ \alpha \cdot \vec{v} = \vec{0} $$ Or, le vecteur nul satisfait cette égalité pour tout scalaire \( \alpha \), même lorsque \( \alpha \ne 0 \) : $$ \alpha \cdot \vec{0} = \vec{0} $$ Par conséquent, le vecteur nul est nécessairement linéairement dépendant.

Et ainsi de suite.