Vecteurs parallèles

Deux vecteurs situés dans un même plan sont dits parallèles lorsqu’ils sont dépendants au sens linéaire.

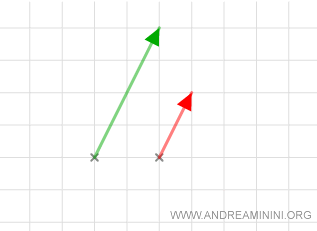
Exemple concret

Considérons deux vecteurs \( v_1 \) et \( v_2 \) appartenant à l’espace vectoriel \( V = \mathbb{R}^2 \), défini sur le corps \( K = \mathbb{R} \) :

$$ v_1 = \overrightarrow{AB} = (2, 4) \\ v_2 = \overrightarrow{CD} = (1, 2) $$

Ces deux vecteurs sont dépendants linéairement si le déterminant de la matrice formée par les vecteurs colonnes est nul :

$$ det \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} = 0 $$

Cela signifie que les deux vecteurs sont proportionnels.

Remarque : Ici, le vecteur \( \overrightarrow{AB} \) est exactement le double du vecteur \( \overrightarrow{CD} \) : $$ \overrightarrow{CD} = 2 \cdot \overrightarrow{AB} = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Le rang de la matrice des vecteurs colonnes est donc au plus égal à 1 :

$$ rg \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} \le 1 $$

Démonstration

Représentons graphiquement les deux vecteurs à partir de l’origine \( O(0,0) \) :

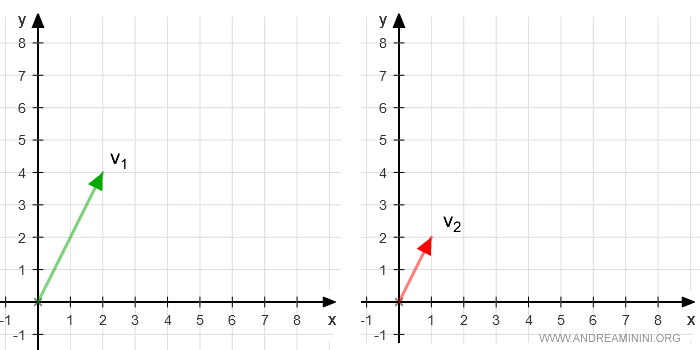
On constate immédiatement que les deux vecteurs sont proportionnels, puisqu’ils se placent sur une même droite passant par l’origine.

L’un est simplement un multiple de l’autre : il existe un scalaire \( k \) tel que \( v_1 = k \cdot v_2 \).

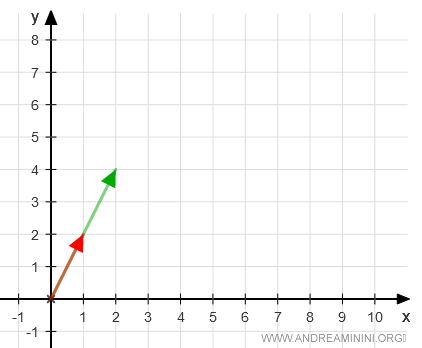
Cela illustre parfaitement la notion de dépendance linéaire entre les deux vecteurs.

Le raisonnement peut être poursuivi de la même manière.

Corollaires

• Vecteur parallèle à une droite

  Un vecteur est parallèle à une droite \( r \) du plan s’il appartient à une droite parallèle à \( r \), ou encore à \( r \) elle-même.

• Vecteur appliqué en un point

  Tout point \( P \) du plan définit un vecteur appliqué \( \overrightarrow{PP} \), lequel est parallèle à n’importe quelle droite du plan.

Vecteurs parallèles dans l’espace

Dans l’espace tridimensionnel \( \mathbb{R}^3 \) :

Un vecteur est parallèle à une droite s’il possède le même vecteur directeur, ou s’il lui est proportionnel.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \\ n \end{pmatrix} $$

Ici, \( (l, m, n) \) désigne le vecteur directeur de la droite dans son équation vectorielle, et \( (x_0, y_0, z_0) \) un point quelconque appartenant à cette droite.

Le vecteur directeur fixe ainsi la direction de toutes les droites parallèles à ce vecteur.

De même, un vecteur est parallèle à un plan dès lors qu’il appartient à un plan parallèle à celui-ci.