Décomposition d’un vecteur

Décomposer un vecteur consiste à l’exprimer à partir de ses composantes le long des axes cartésiens. Autrement dit, un vecteur \( \vec{v} \) peut s’écrire comme la somme de ses composantes \( \vec{v_x} \), \( \vec{v_y} \) et \( \vec{v_z} \) : $$ \vec{v} = \vec{v_x} + \vec{v_y} + \vec{v_z} $$ Il peut aussi se représenter comme une combinaison linéaire de vecteurs unitaires : $$ \vec{v} = \alpha_1 \vec{u_x} + \alpha_2 \vec{u_y} + \alpha_3 \vec{u_z} $$

Ici, les vecteurs unitaires \( u_x \), \( u_y \), \( u_z \) indiquent les directions de référence d’un repère cartésien tridimensionnel (x, y, z).

Les scalaires α₁, α₂, α₃ sont les coefficients qui déterminent la décomposition du vecteur.

Que représentent exactement ces composantes ? Il s’agit des projections du vecteur sur les axes cartésiens. Prenons par exemple les composantes \( \vec{v_x} \) et \( \vec{v_y} \) d’un vecteur \( \vec{v} \) dans un plan cartésien à deux dimensions (x, y).

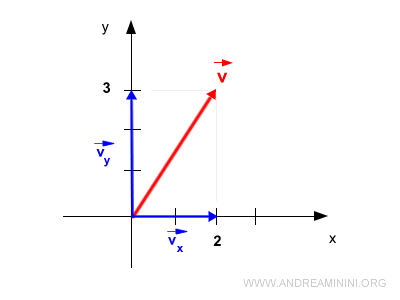
À noter que ces composantes sont elles-mêmes des vecteurs, et non de simples scalaires.

Exemple pratique

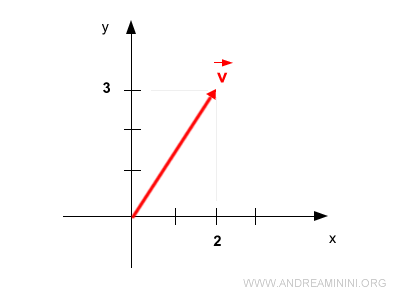
Considérons un vecteur bidimensionnel \( v = (2,3)^T \), que l’on écrit :

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Sa représentation graphique est la suivante :

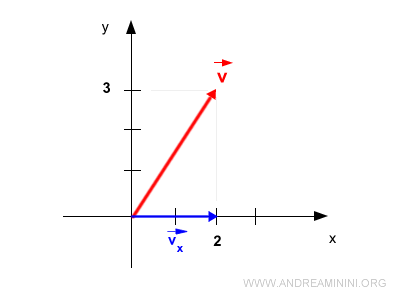
La projection de \( \vec{v} \) sur l’axe x fournit sa composante selon x.

 

De même, sa projection sur l’axe y donne la composante selon y.

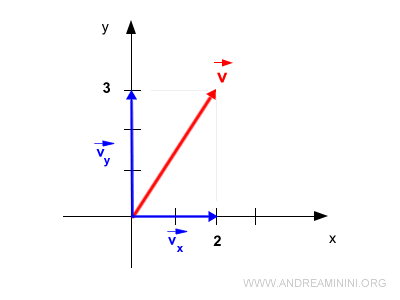
On obtient ainsi deux vecteurs :

$$ \vec{v_x} = \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \quad \vec{v_y} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

Leur somme redonne le vecteur initial :

$$ \vec{v_x} + \vec{v_y} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \vec{v} $$

On peut également exprimer ces composantes comme des multiples de vecteurs unitaires :

$$ \vec{v_x} = x \cdot \vec{u_x}, \quad \vec{v_y} = y \cdot \vec{u_y} $$

Avec x=2 et y=3 :

$$ \vec{v_x} = 2 \cdot \vec{u_x}, \quad \vec{v_y} = 3 \cdot \vec{u_y} $$

Or, dans un repère cartésien, les vecteurs unitaires sont \( \vec{u_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \; \vec{u_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \). On peut donc écrire :

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Cette combinaison linéaire de vecteurs unitaires permet de reconstruire le vecteur \( \vec{v} \).

Remarque. Les normes des composantes \( \vec{v_x} \) et \( \vec{v_y} \) peuvent aussi se calculer grâce aux fonctions trigonométriques : $$ | \vec{v_x} | = r \cdot \sin \Phi, \quad | \vec{v_y} | = r \cdot \cos \Phi $$ où \( \Phi \) est l’angle formé par le vecteur avec l’axe x, et \( r \) la norme du vecteur.

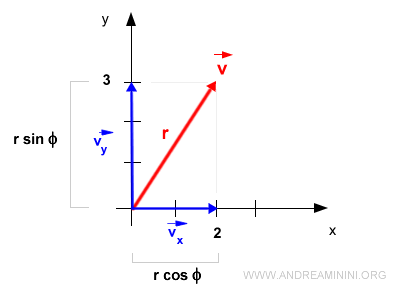
La norme du vecteur se calcule en appliquant le théorème de Pythagore : $$ r = \sqrt{ |\vec{x}|^2 + |\vec{y}|^2 } $$ $$ r = \sqrt{ 2^2 + 3^2 } $$ $$ r = \sqrt{ 4 + 9 } $$ $$ r = \sqrt{ 13 } $$

Exemple 2

Si le vecteur n’a pas pour origine (0,0), il faut calculer ses projections à la fois depuis l’origine et depuis son extrémité.

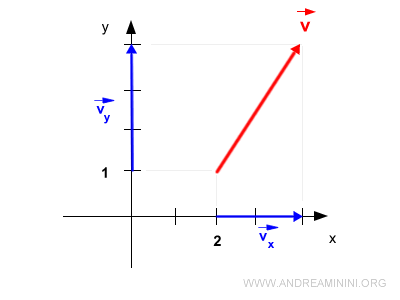
Et ainsi de suite.